Intial Commit
This commit is contained in:
118
nodered/rootfs/data/node_modules/decimal.js/CHANGELOG.md
generated
vendored
Normal file
118
nodered/rootfs/data/node_modules/decimal.js/CHANGELOG.md
generated
vendored
Normal file
@@ -0,0 +1,118 @@
|
||||
#### 7.1.1
|
||||
* 10/01/2017
|
||||
* Remove duplicated for-loop
|
||||
* Minor refactoring
|
||||
|
||||
#### 7.1.0
|
||||
* 09/11/2016
|
||||
* Support ES6 imports.
|
||||
|
||||
#### 7.0.0
|
||||
* 09/11/2016
|
||||
* Remove `require('crypto')` - leave it to the user
|
||||
* Default `Decimal.crypto` to `false`
|
||||
* Add `Decimal.set` as `Decimal.config` alias
|
||||
|
||||
#### 6.0.0
|
||||
* 30/06/2016
|
||||
* Removed base-88 serialization format
|
||||
* Amended `toJSON` and removed `Decimal.fromJSON` accordingly
|
||||
|
||||
#### 5.0.8
|
||||
* 09/03/2016
|
||||
* Add newline to single test results
|
||||
* Correct year
|
||||
|
||||
#### 5.0.7
|
||||
* 29/02/2016
|
||||
* Add decimal.js-light link
|
||||
* Remove outdated example from docs
|
||||
|
||||
#### 5.0.6
|
||||
* 22/02/2016
|
||||
* Add bower.json
|
||||
|
||||
#### 5.0.5
|
||||
* 20/02/2016
|
||||
* Bugfix: #26 wrong precision applied
|
||||
|
||||
#### 5.0.4
|
||||
* 14/02/2016
|
||||
* Bugfix: #26 clone
|
||||
|
||||
#### 5.0.3
|
||||
* 06/02/2016
|
||||
* Refactor tests
|
||||
|
||||
#### 5.0.2
|
||||
* 05/02/2016
|
||||
* Added immutability tests
|
||||
* Minor *decimal.js* clean-up
|
||||
|
||||
#### 5.0.1
|
||||
* 28/01/2016
|
||||
* Bugfix: #20 cos mutates value
|
||||
* Add pi info to docs
|
||||
|
||||
#### 5.0.0
|
||||
* 25/01/2016
|
||||
* Added trigonometric functions and `cubeRoot` method
|
||||
* Added most of JavaScript's `Math` object methods as Decimal methods
|
||||
* Added `toBinary`, `toHexadecimal` and `toOctal` methods
|
||||
* Added `isPositive` method
|
||||
* Removed the 15 significant digit limit for numbers
|
||||
* `toFraction` now returns an array of two Decimals, not two strings
|
||||
* String values containing whitespace or a plus sign are no longer accepted
|
||||
* `valueOf` now returns `'-0'` for minus zero
|
||||
* `comparedTo` now returns `NaN` not `null` for comparisons with `NaN`
|
||||
* `Decimal.max` and `Decimal.min` no longer accept an array
|
||||
* The Decimal constructor and `toString` no longer accept a base argument
|
||||
* Binary, hexadecimal and octal prefixes are now recognised for string values
|
||||
* Removed `Decimal.errors` configuration property
|
||||
* Removed `toFormat` method
|
||||
* Removed `Decimal.ONE`
|
||||
* Renamed `exponential` method to `naturalExponential`
|
||||
* Renamed `Decimal.constructor` method to `Decimal.clone`
|
||||
* Simplified error handling and amended error messages
|
||||
* Refactored the test suite
|
||||
* `Decimal.crypto` is now `undefined` by default, and the `crypto` object will be used if available
|
||||
* Major internal refactoring
|
||||
* Removed *bower.json*
|
||||
|
||||
#### 4.0.2
|
||||
* 20/02/2015 Add bower.json. Add source map. Amend travis CI. Amend doc/comments
|
||||
|
||||
#### 4.0.1
|
||||
* 11/12/2014 Assign correct constructor when duplicating a Decimal
|
||||
|
||||
#### 4.0.0
|
||||
* 10/11/2014 `toFormat` amended to use `Decimal.format` object for more flexible configuration
|
||||
|
||||
#### 3.0.1
|
||||
* 8/06/2014 Surround crypto require in try catch. See issue #5
|
||||
|
||||
#### 3.0.0
|
||||
* 4/06/2014 `random` simplified. Major internal changes mean the properties of a Decimal must now be considered read-only
|
||||
|
||||
#### 2.1.0
|
||||
* 4/06/2014 Amend UMD
|
||||
|
||||
#### 2.0.3
|
||||
* 8/05/2014 Fix NaN toNumber
|
||||
|
||||
#### 2.0.2
|
||||
* 30/04/2014 Correct doc links
|
||||
|
||||
#### 2.0.1
|
||||
* 10/04/2014 Update npmignore
|
||||
|
||||
#### 2.0.0
|
||||
* 10/04/2014 Add `toSignificantDigits`
|
||||
* Remove `toInteger`
|
||||
* No arguments to `ceil`, `floor`, `round` and `trunc`
|
||||
|
||||
#### 1.0.1
|
||||
* 07/04/2014 Minor documentation clean-up
|
||||
|
||||
#### 1.0.0
|
||||
* 02/04/2014 Initial release
|
||||
23
nodered/rootfs/data/node_modules/decimal.js/LICENCE.md
generated
vendored
Normal file
23
nodered/rootfs/data/node_modules/decimal.js/LICENCE.md
generated
vendored
Normal file
@@ -0,0 +1,23 @@
|
||||
The MIT Licence.
|
||||
|
||||
Copyright (c) 2016, 2017 Michael Mclaughlin
|
||||
|
||||
Permission is hereby granted, free of charge, to any person obtaining
|
||||
a copy of this software and associated documentation files (the
|
||||
'Software'), to deal in the Software without restriction, including
|
||||
without limitation the rights to use, copy, modify, merge, publish,
|
||||
distribute, sublicense, and/or sell copies of the Software, and to
|
||||
permit persons to whom the Software is furnished to do so, subject to
|
||||
the following conditions:
|
||||
|
||||
The above copyright notice and this permission notice shall be
|
||||
included in all copies or substantial portions of the Software.
|
||||
|
||||
THE SOFTWARE IS PROVIDED 'AS IS', WITHOUT WARRANTY OF ANY KIND,
|
||||
EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF
|
||||
MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.
|
||||
IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY
|
||||
CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT,
|
||||
TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE
|
||||
SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
|
||||
|
||||
232
nodered/rootfs/data/node_modules/decimal.js/README.md
generated
vendored
Normal file
232
nodered/rootfs/data/node_modules/decimal.js/README.md
generated
vendored
Normal file
@@ -0,0 +1,232 @@
|
||||
|
||||
|
||||
An arbitrary-precision Decimal type for JavaScript.
|
||||
|
||||
<br>
|
||||
[](https://travis-ci.org/MikeMcl/decimal.js)
|
||||
<br>
|
||||
|
||||
## Features
|
||||
|
||||
- Integers and floats
|
||||
- Simple but full-featured API
|
||||
- Replicates many of the methods of JavaScript's `Number.prototype` and `Math` objects
|
||||
- Also handles hexadecimal, binary and octal values
|
||||
- Faster, smaller, and perhaps easier to use than JavaScript versions of Java's BigDecimal
|
||||
- No dependencies
|
||||
- Wide platform compatibility: uses JavaScript 1.5 (ECMAScript 3) features only
|
||||
- Comprehensive [documentation](http://mikemcl.github.io/decimal.js/) and test set
|
||||
|
||||
|
||||
|
||||
The library is similar to [bignumber.js](https://github.com/MikeMcl/bignumber.js/), but here
|
||||
precision is specified in terms of significant digits rather than decimal places, and all
|
||||
calculations are rounded to the precision (similar to Python's decimal module) rather than just
|
||||
those involving division.
|
||||
|
||||
This library also adds the trigonometric functions, among others, and supports non-integer powers,
|
||||
which makes it a significantly larger library than *bignumber.js* and the even smaller
|
||||
[big.js](https://github.com/MikeMcl/big.js/).
|
||||
|
||||
For a lighter version of this library without the trigonometric functions see the
|
||||
[v4.x.x](https://github.com/MikeMcl/decimal.js/tree/v4.x.x) branch where version 4 continues to be supported, or better, see [decimal.js-light](https://github.com/MikeMcl/decimal.js-light/), which is lighter still.
|
||||
|
||||
## Load
|
||||
|
||||
The library is the single JavaScript file *decimal.js* (or minified, *decimal.min.js*).
|
||||
|
||||
It can be loaded using a script tag in an HTML document for the browser
|
||||
|
||||
```html
|
||||
<script src='path/to/decimal.js'></script>
|
||||
```
|
||||
|
||||
or as a [Node.js](http://nodejs.org) module using `require`.
|
||||
|
||||
```js
|
||||
var Decimal = require('decimal.js');
|
||||
```
|
||||
|
||||
For Node, the library is available from the [npm](https://npmjs.org/) registry
|
||||
|
||||
```bash
|
||||
$ npm install decimal.js
|
||||
```
|
||||
|
||||
To load with AMD loader libraries such as [requireJS](http://requirejs.org/):
|
||||
|
||||
```js
|
||||
require(['decimal'], function(Decimal) {
|
||||
// Use Decimal here in local scope. No global Decimal.
|
||||
});
|
||||
```
|
||||
|
||||
## Use
|
||||
|
||||
*In all examples below, `var`, semicolons and `toString` calls are not shown.
|
||||
If a commented-out value is in quotes it means `toString` has been called on the preceding expression.*
|
||||
|
||||
The library exports a single function object, `Decimal`, the constructor of Decimal instances.
|
||||
|
||||
It accepts a value of type number, string or Decimal.
|
||||
|
||||
```js
|
||||
x = new Decimal(123.4567)
|
||||
y = new Decimal('123456.7e-3')
|
||||
z = new Decimal(x)
|
||||
x.equals(y) && y.equals(z) && x.equals(z) // true
|
||||
```
|
||||
|
||||
A value can also be in binary, hexadecimal or octal if the appropriate prefix is included.
|
||||
|
||||
```js
|
||||
x = new Decimal('0xff.f') // '255.9375'
|
||||
y = new Decimal('0b10101100') // '172'
|
||||
z = x.plus(y) // '427.9375'
|
||||
|
||||
z.toBinary() // '0b110101011.1111'
|
||||
z.toBinary(13) // '0b1.101010111111p+8'
|
||||
```
|
||||
|
||||
A Decimal is immutable in the sense that it is not changed by its methods.
|
||||
|
||||
```js
|
||||
0.3 - 0.1 // 0.19999999999999998
|
||||
x = new Decimal(0.3)
|
||||
x.minus(0.1) // '0.2'
|
||||
x // '0.3'
|
||||
```
|
||||
|
||||
The methods that return a Decimal can be chained.
|
||||
|
||||
```js
|
||||
x.dividedBy(y).plus(z).times(9).floor()
|
||||
x.times('1.23456780123456789e+9').plus(9876.5432321).dividedBy('4444562598.111772').ceil()
|
||||
```
|
||||
|
||||
Many method names have a shorter alias.
|
||||
|
||||
```js
|
||||
x.squareRoot().dividedBy(y).toPower(3).equals(x.sqrt().div(y).pow(3)) // true
|
||||
x.cmp(y.mod(z).neg()) == 1 && x.comparedTo(y.modulo(z).negated()) == 1 // true
|
||||
```
|
||||
|
||||
Like JavaScript's Number type, there are `toExponential`, `toFixed` and `toPrecision` methods,
|
||||
|
||||
```js
|
||||
x = new Decimal(255.5)
|
||||
x.toExponential(5) // '2.55500e+2'
|
||||
x.toFixed(5) // '255.50000'
|
||||
x.toPrecision(5) // '255.50'
|
||||
```
|
||||
|
||||
and almost all of the methods of JavaScript's Math object are also replicated.
|
||||
|
||||
```js
|
||||
Decimal.sqrt('6.98372465832e+9823') // '8.3568682281821340204e+4911'
|
||||
Decimal.pow(2, 0.0979843) // '1.0702770511687781839'
|
||||
```
|
||||
|
||||
There are `isNaN` and `isFinite` methods, as `NaN` and `Infinity` are valid `Decimal` values,
|
||||
|
||||
```js
|
||||
x = new Decimal(NaN) // 'NaN'
|
||||
y = new Decimal(Infinity) // 'Infinity'
|
||||
x.isNaN() && !y.isNaN() && !x.isFinite() && !y.isFinite() // true
|
||||
```
|
||||
|
||||
and a `toFraction` method with an optional *maximum denominator* argument
|
||||
|
||||
```js
|
||||
z = new Decimal(355)
|
||||
pi = z.dividedBy(113) // '3.1415929204'
|
||||
pi.toFraction() // [ '7853982301', '2500000000' ]
|
||||
pi.toFraction(1000) // [ '355', '113' ]
|
||||
```
|
||||
|
||||
All calculations are rounded according to the number of significant digits and rounding mode
|
||||
specified by the `precision` and `rounding` properties of the Decimal constructor.
|
||||
|
||||
Multiple Decimal constructors can be created, each with their own independent configuration which
|
||||
applies to all Decimal numbers created from it.
|
||||
|
||||
```js
|
||||
// Set the precision and rounding of the default Decimal constructor
|
||||
Decimal.set({ precision: 5, rounding: 4 })
|
||||
|
||||
// Create another Decimal constructor, optionally passing in a configuration object
|
||||
Decimal10 = Decimal.clone({ precision: 10, rounding: 1 })
|
||||
|
||||
x = new Decimal(5)
|
||||
y = new Decimal10(5)
|
||||
|
||||
x.div(3) // '1.6667'
|
||||
y.div(3) // '1.666666666'
|
||||
```
|
||||
|
||||
The value of a Decimal is stored in a floating point format in terms of its digits, exponent and sign.
|
||||
|
||||
```js
|
||||
x = new Decimal(-12345.67);
|
||||
x.d // [ 12345, 6700000 ] digits (base 10000000)
|
||||
x.e // 4 exponent (base 10)
|
||||
x.s // -1 sign
|
||||
```
|
||||
|
||||
For further information see the [API](http://mikemcl.github.io/decimal.js/) reference in the *doc* directory.
|
||||
|
||||
## Test
|
||||
|
||||
The library can be tested using Node.js or a browser.
|
||||
|
||||
The *test* directory contains the file *test.js* which runs all the tests when executed by Node,
|
||||
and the file *test.html* which runs all the tests when opened in a browser.
|
||||
|
||||
To run all the tests, from a command-line at the root directory using npm
|
||||
|
||||
```bash
|
||||
$ npm test
|
||||
```
|
||||
|
||||
or at the *test* directory using Node
|
||||
|
||||
```bash
|
||||
$ node test
|
||||
```
|
||||
|
||||
Each separate test module can also be executed individually, for example, at the *test/modules* directory
|
||||
|
||||
```bash
|
||||
$ node toFraction
|
||||
```
|
||||
|
||||
## Build
|
||||
|
||||
For Node, if [uglify-js](https://github.com/mishoo/UglifyJS2) is installed
|
||||
|
||||
```bash
|
||||
npm install uglify-js -g
|
||||
```
|
||||
|
||||
then
|
||||
|
||||
```bash
|
||||
npm run build
|
||||
```
|
||||
|
||||
will create *decimal.min.js*, and a source map will also be added to the *doc* directory.
|
||||
|
||||
|
||||
## Feedback
|
||||
|
||||
<a href='mailto:M8ch88l@gmail.com'>M8ch88l@gmail.com</a>
|
||||
|
||||
**BTC** 16MjxmTB5EZxY5Uk9xyhfsu4n9gYxEJYkY
|
||||
|
||||
**Monero** 4B7GE8BUQ5dHjHxVubTDmsTn4bUYWG6bsRXQwunDifX6hcNAfkmGxcZYQGbpYgArKLNxfA15LK2j6bUENiE9eTHRAWkEB5R
|
||||
|
||||
## Licence
|
||||
|
||||
MIT.
|
||||
|
||||
See *LICENCE.md*
|
||||
33
nodered/rootfs/data/node_modules/decimal.js/bower.json
generated
vendored
Normal file
33
nodered/rootfs/data/node_modules/decimal.js/bower.json
generated
vendored
Normal file
@@ -0,0 +1,33 @@
|
||||
{
|
||||
"name": "decimal.js",
|
||||
"main": "decimal.js",
|
||||
"version": "7.1.1",
|
||||
"homepage": "https://github.com/MikeMcl/decimal.js",
|
||||
"authors": [
|
||||
"Michael Mclaughlin <M8ch88l@gmail.com>"
|
||||
],
|
||||
"description": "An arbitrary-precision Decimal type for JavaScript",
|
||||
"moduleType": [
|
||||
"amd",
|
||||
"globals",
|
||||
"node"
|
||||
],
|
||||
"keywords": [
|
||||
"arbitrary",
|
||||
"precision",
|
||||
"arithmetic",
|
||||
"bignumber",
|
||||
"decimal",
|
||||
"float",
|
||||
"biginteger",
|
||||
"bigdecimal",
|
||||
"bignum",
|
||||
"math"
|
||||
],
|
||||
"license": "MIT",
|
||||
"ignore": [
|
||||
".*",
|
||||
"*.json",
|
||||
"test"
|
||||
]
|
||||
}
|
||||
4799
nodered/rootfs/data/node_modules/decimal.js/decimal.js
generated
vendored
Normal file
4799
nodered/rootfs/data/node_modules/decimal.js/decimal.js
generated
vendored
Normal file
@@ -0,0 +1,4799 @@
|
||||
/*! decimal.js v7.1.1 https://github.com/MikeMcl/decimal.js/LICENCE */
|
||||
;(function (globalScope) {
|
||||
'use strict';
|
||||
|
||||
|
||||
/*
|
||||
* decimal.js v7.1.1
|
||||
* An arbitrary-precision Decimal type for JavaScript.
|
||||
* https://github.com/MikeMcl/decimal.js
|
||||
* Copyright (c) 2016 Michael Mclaughlin <M8ch88l@gmail.com>
|
||||
* MIT Licence
|
||||
*/
|
||||
|
||||
|
||||
// ----------------------------------- EDITABLE DEFAULTS ------------------------------------ //
|
||||
|
||||
|
||||
// The maximum exponent magnitude.
|
||||
// The limit on the value of `toExpNeg`, `toExpPos`, `minE` and `maxE`.
|
||||
var EXP_LIMIT = 9e15, // 0 to 9e15
|
||||
|
||||
// The limit on the value of `precision`, and on the value of the first argument to
|
||||
// `toDecimalPlaces`, `toExponential`, `toFixed`, `toPrecision` and `toSignificantDigits`.
|
||||
MAX_DIGITS = 1e9, // 0 to 1e9
|
||||
|
||||
// Base conversion alphabet.
|
||||
NUMERALS = '0123456789abcdef',
|
||||
|
||||
// The natural logarithm of 10 (1025 digits).
|
||||
LN10 = '2.3025850929940456840179914546843642076011014886287729760333279009675726096773524802359972050895982983419677840422862486334095254650828067566662873690987816894829072083255546808437998948262331985283935053089653777326288461633662222876982198867465436674744042432743651550489343149393914796194044002221051017141748003688084012647080685567743216228355220114804663715659121373450747856947683463616792101806445070648000277502684916746550586856935673420670581136429224554405758925724208241314695689016758940256776311356919292033376587141660230105703089634572075440370847469940168269282808481184289314848524948644871927809676271275775397027668605952496716674183485704422507197965004714951050492214776567636938662976979522110718264549734772662425709429322582798502585509785265383207606726317164309505995087807523710333101197857547331541421808427543863591778117054309827482385045648019095610299291824318237525357709750539565187697510374970888692180205189339507238539205144634197265287286965110862571492198849978748873771345686209167058',
|
||||
|
||||
// Pi (1025 digits).
|
||||
PI = '3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632789',
|
||||
|
||||
|
||||
// The initial configuration properties of the Decimal constructor.
|
||||
Decimal = {
|
||||
|
||||
// These values must be integers within the stated ranges (inclusive).
|
||||
// Most of these values can be changed at run-time using the `Decimal.config` method.
|
||||
|
||||
// The maximum number of significant digits of the result of a calculation or base conversion.
|
||||
// E.g. `Decimal.config({ precision: 20 });`
|
||||
precision: 20, // 1 to MAX_DIGITS
|
||||
|
||||
// The rounding mode used when rounding to `precision`.
|
||||
//
|
||||
// ROUND_UP 0 Away from zero.
|
||||
// ROUND_DOWN 1 Towards zero.
|
||||
// ROUND_CEIL 2 Towards +Infinity.
|
||||
// ROUND_FLOOR 3 Towards -Infinity.
|
||||
// ROUND_HALF_UP 4 Towards nearest neighbour. If equidistant, up.
|
||||
// ROUND_HALF_DOWN 5 Towards nearest neighbour. If equidistant, down.
|
||||
// ROUND_HALF_EVEN 6 Towards nearest neighbour. If equidistant, towards even neighbour.
|
||||
// ROUND_HALF_CEIL 7 Towards nearest neighbour. If equidistant, towards +Infinity.
|
||||
// ROUND_HALF_FLOOR 8 Towards nearest neighbour. If equidistant, towards -Infinity.
|
||||
//
|
||||
// E.g.
|
||||
// `Decimal.rounding = 4;`
|
||||
// `Decimal.rounding = Decimal.ROUND_HALF_UP;`
|
||||
rounding: 4, // 0 to 8
|
||||
|
||||
// The modulo mode used when calculating the modulus: a mod n.
|
||||
// The quotient (q = a / n) is calculated according to the corresponding rounding mode.
|
||||
// The remainder (r) is calculated as: r = a - n * q.
|
||||
//
|
||||
// UP 0 The remainder is positive if the dividend is negative, else is negative.
|
||||
// DOWN 1 The remainder has the same sign as the dividend (JavaScript %).
|
||||
// FLOOR 3 The remainder has the same sign as the divisor (Python %).
|
||||
// HALF_EVEN 6 The IEEE 754 remainder function.
|
||||
// EUCLID 9 Euclidian division. q = sign(n) * floor(a / abs(n)). Always positive.
|
||||
//
|
||||
// Truncated division (1), floored division (3), the IEEE 754 remainder (6), and Euclidian
|
||||
// division (9) are commonly used for the modulus operation. The other rounding modes can also
|
||||
// be used, but they may not give useful results.
|
||||
modulo: 1, // 0 to 9
|
||||
|
||||
// The exponent value at and beneath which `toString` returns exponential notation.
|
||||
// JavaScript numbers: -7
|
||||
toExpNeg: -7, // 0 to -EXP_LIMIT
|
||||
|
||||
// The exponent value at and above which `toString` returns exponential notation.
|
||||
// JavaScript numbers: 21
|
||||
toExpPos: 21, // 0 to EXP_LIMIT
|
||||
|
||||
// The minimum exponent value, beneath which underflow to zero occurs.
|
||||
// JavaScript numbers: -324 (5e-324)
|
||||
minE: -EXP_LIMIT, // -1 to -EXP_LIMIT
|
||||
|
||||
// The maximum exponent value, above which overflow to Infinity occurs.
|
||||
// JavaScript numbers: 308 (1.7976931348623157e+308)
|
||||
maxE: EXP_LIMIT, // 1 to EXP_LIMIT
|
||||
|
||||
// Whether to use cryptographically-secure random number generation, if available.
|
||||
crypto: false // true/false
|
||||
},
|
||||
|
||||
|
||||
// ----------------------------------- END OF EDITABLE DEFAULTS ------------------------------- //
|
||||
|
||||
|
||||
inexact, noConflict, quadrant,
|
||||
external = true,
|
||||
|
||||
decimalError = '[DecimalError] ',
|
||||
invalidArgument = decimalError + 'Invalid argument: ',
|
||||
precisionLimitExceeded = decimalError + 'Precision limit exceeded',
|
||||
cryptoUnavailable = decimalError + 'crypto unavailable',
|
||||
|
||||
mathfloor = Math.floor,
|
||||
mathpow = Math.pow,
|
||||
|
||||
isBinary = /^0b([01]+(\.[01]*)?|\.[01]+)(p[+-]?\d+)?$/i,
|
||||
isHex = /^0x([0-9a-f]+(\.[0-9a-f]*)?|\.[0-9a-f]+)(p[+-]?\d+)?$/i,
|
||||
isOctal = /^0o([0-7]+(\.[0-7]*)?|\.[0-7]+)(p[+-]?\d+)?$/i,
|
||||
isDecimal = /^(\d+(\.\d*)?|\.\d+)(e[+-]?\d+)?$/i,
|
||||
|
||||
BASE = 1e7,
|
||||
LOG_BASE = 7,
|
||||
MAX_SAFE_INTEGER = 9007199254740991,
|
||||
|
||||
LN10_PRECISION = LN10.length - 1,
|
||||
PI_PRECISION = PI.length - 1,
|
||||
|
||||
// Decimal.prototype object
|
||||
P = {};
|
||||
|
||||
|
||||
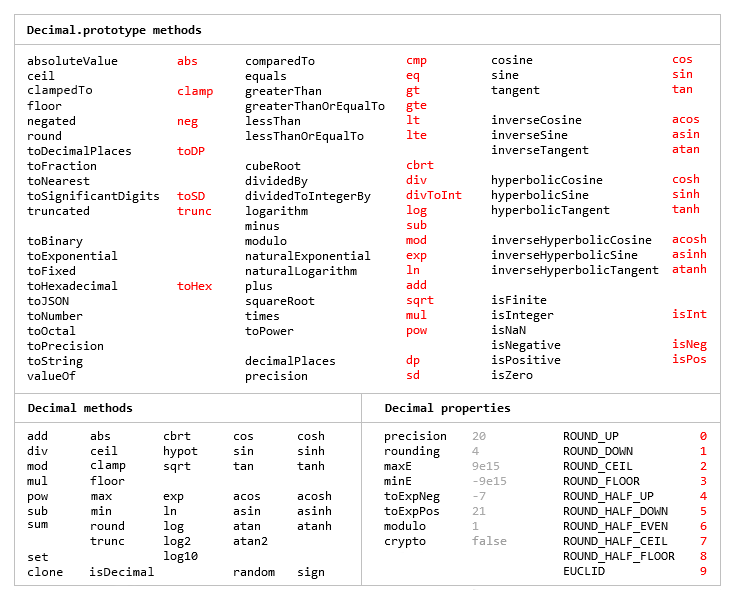
// Decimal prototype methods
|
||||
|
||||
|
||||
/*
|
||||
* absoluteValue abs
|
||||
* ceil
|
||||
* comparedTo cmp
|
||||
* cosine cos
|
||||
* cubeRoot cbrt
|
||||
* decimalPlaces dp
|
||||
* dividedBy div
|
||||
* dividedToIntegerBy divToInt
|
||||
* equals eq
|
||||
* floor
|
||||
* greaterThan gt
|
||||
* greaterThanOrEqualTo gte
|
||||
* hyperbolicCosine cosh
|
||||
* hyperbolicSine sinh
|
||||
* hyperbolicTangent tanh
|
||||
* inverseCosine acos
|
||||
* inverseHyperbolicCosine acosh
|
||||
* inverseHyperbolicSine asinh
|
||||
* inverseHyperbolicTangent atanh
|
||||
* inverseSine asin
|
||||
* inverseTangent atan
|
||||
* isFinite
|
||||
* isInteger isInt
|
||||
* isNaN
|
||||
* isNegative isNeg
|
||||
* isPositive isPos
|
||||
* isZero
|
||||
* lessThan lt
|
||||
* lessThanOrEqualTo lte
|
||||
* logarithm log
|
||||
* [maximum] [max]
|
||||
* [minimum] [min]
|
||||
* minus sub
|
||||
* modulo mod
|
||||
* naturalExponential exp
|
||||
* naturalLogarithm ln
|
||||
* negated neg
|
||||
* plus add
|
||||
* precision sd
|
||||
* round
|
||||
* sine sin
|
||||
* squareRoot sqrt
|
||||
* tangent tan
|
||||
* times mul
|
||||
* toBinary
|
||||
* toDecimalPlaces toDP
|
||||
* toExponential
|
||||
* toFixed
|
||||
* toFraction
|
||||
* toHexadecimal toHex
|
||||
* toNearest
|
||||
* toNumber
|
||||
* toOctal
|
||||
* toPower pow
|
||||
* toPrecision
|
||||
* toSignificantDigits toSD
|
||||
* toString
|
||||
* truncated trunc
|
||||
* valueOf toJSON
|
||||
*/
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the absolute value of this Decimal.
|
||||
*
|
||||
*/
|
||||
P.absoluteValue = P.abs = function () {
|
||||
var x = new this.constructor(this);
|
||||
if (x.s < 0) x.s = 1;
|
||||
return finalise(x);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal rounded to a whole number in the
|
||||
* direction of positive Infinity.
|
||||
*
|
||||
*/
|
||||
P.ceil = function () {
|
||||
return finalise(new this.constructor(this), this.e + 1, 2);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return
|
||||
* 1 if the value of this Decimal is greater than the value of `y`,
|
||||
* -1 if the value of this Decimal is less than the value of `y`,
|
||||
* 0 if they have the same value,
|
||||
* NaN if the value of either Decimal is NaN.
|
||||
*
|
||||
*/
|
||||
P.comparedTo = P.cmp = function (y) {
|
||||
var i, j, xdL, ydL,
|
||||
x = this,
|
||||
xd = x.d,
|
||||
yd = (y = new x.constructor(y)).d,
|
||||
xs = x.s,
|
||||
ys = y.s;
|
||||
|
||||
// Either NaN or ±Infinity?
|
||||
if (!xd || !yd) {
|
||||
return !xs || !ys ? NaN : xs !== ys ? xs : xd === yd ? 0 : !xd ^ xs < 0 ? 1 : -1;
|
||||
}
|
||||
|
||||
// Either zero?
|
||||
if (!xd[0] || !yd[0]) return xd[0] ? xs : yd[0] ? -ys : 0;
|
||||
|
||||
// Signs differ?
|
||||
if (xs !== ys) return xs;
|
||||
|
||||
// Compare exponents.
|
||||
if (x.e !== y.e) return x.e > y.e ^ xs < 0 ? 1 : -1;
|
||||
|
||||
xdL = xd.length;
|
||||
ydL = yd.length;
|
||||
|
||||
// Compare digit by digit.
|
||||
for (i = 0, j = xdL < ydL ? xdL : ydL; i < j; ++i) {
|
||||
if (xd[i] !== yd[i]) return xd[i] > yd[i] ^ xs < 0 ? 1 : -1;
|
||||
}
|
||||
|
||||
// Compare lengths.
|
||||
return xdL === ydL ? 0 : xdL > ydL ^ xs < 0 ? 1 : -1;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the cosine of the value in radians of this Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-1, 1]
|
||||
*
|
||||
* cos(0) = 1
|
||||
* cos(-0) = 1
|
||||
* cos(Infinity) = NaN
|
||||
* cos(-Infinity) = NaN
|
||||
* cos(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.cosine = P.cos = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.d) return new Ctor(NaN);
|
||||
|
||||
// cos(0) = cos(-0) = 1
|
||||
if (!x.d[0]) return new Ctor(1);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + Math.max(x.e, x.sd()) + LOG_BASE;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = cosine(Ctor, toLessThanHalfPi(Ctor, x));
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return finalise(quadrant == 2 || quadrant == 3 ? x.neg() : x, pr, rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
*
|
||||
* Return a new Decimal whose value is the cube root of the value of this Decimal, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* cbrt(0) = 0
|
||||
* cbrt(-0) = -0
|
||||
* cbrt(1) = 1
|
||||
* cbrt(-1) = -1
|
||||
* cbrt(N) = N
|
||||
* cbrt(-I) = -I
|
||||
* cbrt(I) = I
|
||||
*
|
||||
* Math.cbrt(x) = (x < 0 ? -Math.pow(-x, 1/3) : Math.pow(x, 1/3))
|
||||
*
|
||||
*/
|
||||
P.cubeRoot = P.cbrt = function () {
|
||||
var e, m, n, r, rep, s, sd, t, t3, t3plusx,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite() || x.isZero()) return new Ctor(x);
|
||||
external = false;
|
||||
|
||||
// Initial estimate.
|
||||
s = x.s * Math.pow(x.s * x, 1 / 3);
|
||||
|
||||
// Math.cbrt underflow/overflow?
|
||||
// Pass x to Math.pow as integer, then adjust the exponent of the result.
|
||||
if (!s || Math.abs(s) == 1 / 0) {
|
||||
n = digitsToString(x.d);
|
||||
e = x.e;
|
||||
|
||||
// Adjust n exponent so it is a multiple of 3 away from x exponent.
|
||||
if (s = (e - n.length + 1) % 3) n += (s == 1 || s == -2 ? '0' : '00');
|
||||
s = Math.pow(n, 1 / 3);
|
||||
|
||||
// Rarely, e may be one less than the result exponent value.
|
||||
e = mathfloor((e + 1) / 3) - (e % 3 == (e < 0 ? -1 : 2));
|
||||
|
||||
if (s == 1 / 0) {
|
||||
n = '5e' + e;
|
||||
} else {
|
||||
n = s.toExponential();
|
||||
n = n.slice(0, n.indexOf('e') + 1) + e;
|
||||
}
|
||||
|
||||
r = new Ctor(n);
|
||||
r.s = x.s;
|
||||
} else {
|
||||
r = new Ctor(s.toString());
|
||||
}
|
||||
|
||||
sd = (e = Ctor.precision) + 3;
|
||||
|
||||
// Halley's method.
|
||||
// TODO? Compare Newton's method.
|
||||
for (;;) {
|
||||
t = r;
|
||||
t3 = t.times(t).times(t);
|
||||
t3plusx = t3.plus(x);
|
||||
r = divide(t3plusx.plus(x).times(t), t3plusx.plus(t3), sd + 2, 1);
|
||||
|
||||
// TODO? Replace with for-loop and checkRoundingDigits.
|
||||
if (digitsToString(t.d).slice(0, sd) === (n = digitsToString(r.d)).slice(0, sd)) {
|
||||
n = n.slice(sd - 3, sd + 1);
|
||||
|
||||
// The 4th rounding digit may be in error by -1 so if the 4 rounding digits are 9999 or 4999
|
||||
// , i.e. approaching a rounding boundary, continue the iteration.
|
||||
if (n == '9999' || !rep && n == '4999') {
|
||||
|
||||
// On the first iteration only, check to see if rounding up gives the exact result as the
|
||||
// nines may infinitely repeat.
|
||||
if (!rep) {
|
||||
finalise(t, e + 1, 0);
|
||||
|
||||
if (t.times(t).times(t).eq(x)) {
|
||||
r = t;
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
sd += 4;
|
||||
rep = 1;
|
||||
} else {
|
||||
|
||||
// If the rounding digits are null, 0{0,4} or 50{0,3}, check for an exact result.
|
||||
// If not, then there are further digits and m will be truthy.
|
||||
if (!+n || !+n.slice(1) && n.charAt(0) == '5') {
|
||||
|
||||
// Truncate to the first rounding digit.
|
||||
finalise(r, e + 1, 1);
|
||||
m = !r.times(r).times(r).eq(x);
|
||||
}
|
||||
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
external = true;
|
||||
|
||||
return finalise(r, e, Ctor.rounding, m);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return the number of decimal places of the value of this Decimal.
|
||||
*
|
||||
*/
|
||||
P.decimalPlaces = P.dp = function () {
|
||||
var w,
|
||||
d = this.d,
|
||||
n = NaN;
|
||||
|
||||
if (d) {
|
||||
w = d.length - 1;
|
||||
n = (w - mathfloor(this.e / LOG_BASE)) * LOG_BASE;
|
||||
|
||||
// Subtract the number of trailing zeros of the last word.
|
||||
w = d[w];
|
||||
if (w) for (; w % 10 == 0; w /= 10) n--;
|
||||
if (n < 0) n = 0;
|
||||
}
|
||||
|
||||
return n;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* n / 0 = I
|
||||
* n / N = N
|
||||
* n / I = 0
|
||||
* 0 / n = 0
|
||||
* 0 / 0 = N
|
||||
* 0 / N = N
|
||||
* 0 / I = 0
|
||||
* N / n = N
|
||||
* N / 0 = N
|
||||
* N / N = N
|
||||
* N / I = N
|
||||
* I / n = I
|
||||
* I / 0 = I
|
||||
* I / N = N
|
||||
* I / I = N
|
||||
*
|
||||
* Return a new Decimal whose value is the value of this Decimal divided by `y`, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.dividedBy = P.div = function (y) {
|
||||
return divide(this, new this.constructor(y));
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the integer part of dividing the value of this Decimal
|
||||
* by the value of `y`, rounded to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.dividedToIntegerBy = P.divToInt = function (y) {
|
||||
var x = this,
|
||||
Ctor = x.constructor;
|
||||
return finalise(divide(x, new Ctor(y), 0, 1, 1), Ctor.precision, Ctor.rounding);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is equal to the value of `y`, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.equals = P.eq = function (y) {
|
||||
return this.cmp(y) === 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal rounded to a whole number in the
|
||||
* direction of negative Infinity.
|
||||
*
|
||||
*/
|
||||
P.floor = function () {
|
||||
return finalise(new this.constructor(this), this.e + 1, 3);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is greater than the value of `y`, otherwise return
|
||||
* false.
|
||||
*
|
||||
*/
|
||||
P.greaterThan = P.gt = function (y) {
|
||||
return this.cmp(y) > 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is greater than or equal to the value of `y`,
|
||||
* otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.greaterThanOrEqualTo = P.gte = function (y) {
|
||||
var k = this.cmp(y);
|
||||
return k == 1 || k === 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic cosine of the value in radians of this
|
||||
* Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [1, Infinity]
|
||||
*
|
||||
* cosh(x) = 1 + x^2/2! + x^4/4! + x^6/6! + ...
|
||||
*
|
||||
* cosh(0) = 1
|
||||
* cosh(-0) = 1
|
||||
* cosh(Infinity) = Infinity
|
||||
* cosh(-Infinity) = Infinity
|
||||
* cosh(NaN) = NaN
|
||||
*
|
||||
* x time taken (ms) result
|
||||
* 1000 9 9.8503555700852349694e+433
|
||||
* 10000 25 4.4034091128314607936e+4342
|
||||
* 100000 171 1.4033316802130615897e+43429
|
||||
* 1000000 3817 1.5166076984010437725e+434294
|
||||
* 10000000 abandoned after 2 minute wait
|
||||
*
|
||||
* TODO? Compare performance of cosh(x) = 0.5 * (exp(x) + exp(-x))
|
||||
*
|
||||
*/
|
||||
P.hyperbolicCosine = P.cosh = function () {
|
||||
var k, n, pr, rm, len,
|
||||
x = this,
|
||||
Ctor = x.constructor,
|
||||
one = new Ctor(1);
|
||||
|
||||
if (!x.isFinite()) return new Ctor(x.s ? 1 / 0 : NaN);
|
||||
if (x.isZero()) return one;
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + Math.max(x.e, x.sd()) + 4;
|
||||
Ctor.rounding = 1;
|
||||
len = x.d.length;
|
||||
|
||||
// Argument reduction: cos(4x) = 1 - 8cos^2(x) + 8cos^4(x) + 1
|
||||
// i.e. cos(x) = 1 - cos^2(x/4)(8 - 8cos^2(x/4))
|
||||
|
||||
// Estimate the optimum number of times to use the argument reduction.
|
||||
// TODO? Estimation reused from cosine() and may not be optimal here.
|
||||
if (len < 32) {
|
||||
k = Math.ceil(len / 3);
|
||||
n = Math.pow(4, -k).toString();
|
||||
} else {
|
||||
k = 16;
|
||||
n = '2.3283064365386962890625e-10';
|
||||
}
|
||||
|
||||
x = taylorSeries(Ctor, 1, x.times(n), new Ctor(1), true);
|
||||
|
||||
// Reverse argument reduction
|
||||
var cosh2_x,
|
||||
i = k,
|
||||
d8 = new Ctor(8);
|
||||
for (; i--;) {
|
||||
cosh2_x = x.times(x);
|
||||
x = one.minus(cosh2_x.times(d8.minus(cosh2_x.times(d8))));
|
||||
}
|
||||
|
||||
return finalise(x, Ctor.precision = pr, Ctor.rounding = rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic sine of the value in radians of this
|
||||
* Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-Infinity, Infinity]
|
||||
*
|
||||
* sinh(x) = x + x^3/3! + x^5/5! + x^7/7! + ...
|
||||
*
|
||||
* sinh(0) = 0
|
||||
* sinh(-0) = -0
|
||||
* sinh(Infinity) = Infinity
|
||||
* sinh(-Infinity) = -Infinity
|
||||
* sinh(NaN) = NaN
|
||||
*
|
||||
* x time taken (ms)
|
||||
* 10 2 ms
|
||||
* 100 5 ms
|
||||
* 1000 14 ms
|
||||
* 10000 82 ms
|
||||
* 100000 886 ms 1.4033316802130615897e+43429
|
||||
* 200000 2613 ms
|
||||
* 300000 5407 ms
|
||||
* 400000 8824 ms
|
||||
* 500000 13026 ms 8.7080643612718084129e+217146
|
||||
* 1000000 48543 ms
|
||||
*
|
||||
* TODO? Compare performance of sinh(x) = 0.5 * (exp(x) - exp(-x))
|
||||
*
|
||||
*/
|
||||
P.hyperbolicSine = P.sinh = function () {
|
||||
var k, pr, rm, len,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite() || x.isZero()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + Math.max(x.e, x.sd()) + 4;
|
||||
Ctor.rounding = 1;
|
||||
len = x.d.length;
|
||||
|
||||
if (len < 3) {
|
||||
x = taylorSeries(Ctor, 2, x, x, true);
|
||||
} else {
|
||||
|
||||
// Alternative argument reduction: sinh(3x) = sinh(x)(3 + 4sinh^2(x))
|
||||
// i.e. sinh(x) = sinh(x/3)(3 + 4sinh^2(x/3))
|
||||
// 3 multiplications and 1 addition
|
||||
|
||||
// Argument reduction: sinh(5x) = sinh(x)(5 + sinh^2(x)(20 + 16sinh^2(x)))
|
||||
// i.e. sinh(x) = sinh(x/5)(5 + sinh^2(x/5)(20 + 16sinh^2(x/5)))
|
||||
// 4 multiplications and 2 additions
|
||||
|
||||
// Estimate the optimum number of times to use the argument reduction.
|
||||
k = 1.4 * Math.sqrt(len);
|
||||
k = k > 16 ? 16 : k | 0;
|
||||
|
||||
x = x.times(Math.pow(5, -k));
|
||||
|
||||
x = taylorSeries(Ctor, 2, x, x, true);
|
||||
|
||||
// Reverse argument reduction
|
||||
var sinh2_x,
|
||||
d5 = new Ctor(5),
|
||||
d16 = new Ctor(16),
|
||||
d20 = new Ctor(20);
|
||||
for (; k--;) {
|
||||
sinh2_x = x.times(x);
|
||||
x = x.times(d5.plus(sinh2_x.times(d16.times(sinh2_x).plus(d20))));
|
||||
}
|
||||
}
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return finalise(x, pr, rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic tangent of the value in radians of this
|
||||
* Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-1, 1]
|
||||
*
|
||||
* tanh(x) = sinh(x) / cosh(x)
|
||||
*
|
||||
* tanh(0) = 0
|
||||
* tanh(-0) = -0
|
||||
* tanh(Infinity) = 1
|
||||
* tanh(-Infinity) = -1
|
||||
* tanh(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.hyperbolicTangent = P.tanh = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite()) return new Ctor(x.s);
|
||||
if (x.isZero()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + 7;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
return divide(x.sinh(), x.cosh(), Ctor.precision = pr, Ctor.rounding = rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arccosine (inverse cosine) in radians of the value of
|
||||
* this Decimal.
|
||||
*
|
||||
* Domain: [-1, 1]
|
||||
* Range: [0, pi]
|
||||
*
|
||||
* acos(x) = pi/2 - asin(x)
|
||||
*
|
||||
* acos(0) = pi/2
|
||||
* acos(-0) = pi/2
|
||||
* acos(1) = 0
|
||||
* acos(-1) = pi
|
||||
* acos(1/2) = pi/3
|
||||
* acos(-1/2) = 2*pi/3
|
||||
* acos(|x| > 1) = NaN
|
||||
* acos(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.inverseCosine = P.acos = function () {
|
||||
var halfPi,
|
||||
x = this,
|
||||
Ctor = x.constructor,
|
||||
k = x.abs().cmp(1),
|
||||
pr = Ctor.precision,
|
||||
rm = Ctor.rounding;
|
||||
|
||||
if (k !== -1) {
|
||||
return k === 0
|
||||
// |x| is 1
|
||||
? x.isNeg() ? getPi(Ctor, pr, rm) : new Ctor(0)
|
||||
// |x| > 1 or x is NaN
|
||||
: new Ctor(NaN);
|
||||
}
|
||||
|
||||
if (x.isZero()) return getPi(Ctor, pr + 4, rm).times(0.5);
|
||||
|
||||
// TODO? Special case acos(0.5) = pi/3 and acos(-0.5) = 2*pi/3
|
||||
|
||||
Ctor.precision = pr + 6;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = x.asin();
|
||||
halfPi = getPi(Ctor, pr + 4, rm).times(0.5);
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return halfPi.minus(x);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic cosine in radians of the
|
||||
* value of this Decimal.
|
||||
*
|
||||
* Domain: [1, Infinity]
|
||||
* Range: [0, Infinity]
|
||||
*
|
||||
* acosh(x) = ln(x + sqrt(x^2 - 1))
|
||||
*
|
||||
* acosh(x < 1) = NaN
|
||||
* acosh(NaN) = NaN
|
||||
* acosh(Infinity) = Infinity
|
||||
* acosh(-Infinity) = NaN
|
||||
* acosh(0) = NaN
|
||||
* acosh(-0) = NaN
|
||||
* acosh(1) = 0
|
||||
* acosh(-1) = NaN
|
||||
*
|
||||
*/
|
||||
P.inverseHyperbolicCosine = P.acosh = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (x.lte(1)) return new Ctor(x.eq(1) ? 0 : NaN);
|
||||
if (!x.isFinite()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + Math.max(Math.abs(x.e), x.sd()) + 4;
|
||||
Ctor.rounding = 1;
|
||||
external = false;
|
||||
|
||||
x = x.times(x).minus(1).sqrt().plus(x);
|
||||
|
||||
external = true;
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return x.ln();
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic sine in radians of the value
|
||||
* of this Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-Infinity, Infinity]
|
||||
*
|
||||
* asinh(x) = ln(x + sqrt(x^2 + 1))
|
||||
*
|
||||
* asinh(NaN) = NaN
|
||||
* asinh(Infinity) = Infinity
|
||||
* asinh(-Infinity) = -Infinity
|
||||
* asinh(0) = 0
|
||||
* asinh(-0) = -0
|
||||
*
|
||||
*/
|
||||
P.inverseHyperbolicSine = P.asinh = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite() || x.isZero()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + 2 * Math.max(Math.abs(x.e), x.sd()) + 6;
|
||||
Ctor.rounding = 1;
|
||||
external = false;
|
||||
|
||||
x = x.times(x).plus(1).sqrt().plus(x);
|
||||
|
||||
external = true;
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return x.ln();
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic tangent in radians of the
|
||||
* value of this Decimal.
|
||||
*
|
||||
* Domain: [-1, 1]
|
||||
* Range: [-Infinity, Infinity]
|
||||
*
|
||||
* atanh(x) = 0.5 * ln((1 + x) / (1 - x))
|
||||
*
|
||||
* atanh(|x| > 1) = NaN
|
||||
* atanh(NaN) = NaN
|
||||
* atanh(Infinity) = NaN
|
||||
* atanh(-Infinity) = NaN
|
||||
* atanh(0) = 0
|
||||
* atanh(-0) = -0
|
||||
* atanh(1) = Infinity
|
||||
* atanh(-1) = -Infinity
|
||||
*
|
||||
*/
|
||||
P.inverseHyperbolicTangent = P.atanh = function () {
|
||||
var pr, rm, wpr, xsd,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite()) return new Ctor(NaN);
|
||||
if (x.e >= 0) return new Ctor(x.abs().eq(1) ? x.s / 0 : x.isZero() ? x : NaN);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
xsd = x.sd();
|
||||
|
||||
if (Math.max(xsd, pr) < 2 * -x.e - 1) return finalise(new Ctor(x), pr, rm, true);
|
||||
|
||||
Ctor.precision = wpr = xsd - x.e;
|
||||
|
||||
x = divide(x.plus(1), new Ctor(1).minus(x), wpr + pr, 1);
|
||||
|
||||
Ctor.precision = pr + 4;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = x.ln();
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return x.times(0.5);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arcsine (inverse sine) in radians of the value of this
|
||||
* Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-pi/2, pi/2]
|
||||
*
|
||||
* asin(x) = 2*atan(x/(1 + sqrt(1 - x^2)))
|
||||
*
|
||||
* asin(0) = 0
|
||||
* asin(-0) = -0
|
||||
* asin(1/2) = pi/6
|
||||
* asin(-1/2) = -pi/6
|
||||
* asin(1) = pi/2
|
||||
* asin(-1) = -pi/2
|
||||
* asin(|x| > 1) = NaN
|
||||
* asin(NaN) = NaN
|
||||
*
|
||||
* TODO? Compare performance of Taylor series.
|
||||
*
|
||||
*/
|
||||
P.inverseSine = P.asin = function () {
|
||||
var halfPi, k,
|
||||
pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (x.isZero()) return new Ctor(x);
|
||||
|
||||
k = x.abs().cmp(1);
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
|
||||
if (k !== -1) {
|
||||
|
||||
// |x| is 1
|
||||
if (k === 0) {
|
||||
halfPi = getPi(Ctor, pr + 4, rm).times(0.5);
|
||||
halfPi.s = x.s;
|
||||
return halfPi;
|
||||
}
|
||||
|
||||
// |x| > 1 or x is NaN
|
||||
return new Ctor(NaN);
|
||||
}
|
||||
|
||||
// TODO? Special case asin(1/2) = pi/6 and asin(-1/2) = -pi/6
|
||||
|
||||
Ctor.precision = pr + 6;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = x.div(new Ctor(1).minus(x.times(x)).sqrt().plus(1)).atan();
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return x.times(2);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arctangent (inverse tangent) in radians of the value
|
||||
* of this Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-pi/2, pi/2]
|
||||
*
|
||||
* atan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
|
||||
*
|
||||
* atan(0) = 0
|
||||
* atan(-0) = -0
|
||||
* atan(1) = pi/4
|
||||
* atan(-1) = -pi/4
|
||||
* atan(Infinity) = pi/2
|
||||
* atan(-Infinity) = -pi/2
|
||||
* atan(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.inverseTangent = P.atan = function () {
|
||||
var i, j, k, n, px, t, r, wpr, x2,
|
||||
x = this,
|
||||
Ctor = x.constructor,
|
||||
pr = Ctor.precision,
|
||||
rm = Ctor.rounding;
|
||||
|
||||
if (!x.isFinite()) {
|
||||
if (!x.s) return new Ctor(NaN);
|
||||
if (pr + 4 <= PI_PRECISION) {
|
||||
r = getPi(Ctor, pr + 4, rm).times(0.5);
|
||||
r.s = x.s;
|
||||
return r;
|
||||
}
|
||||
} else if (x.isZero()) {
|
||||
return new Ctor(x);
|
||||
} else if (x.abs().eq(1) && pr + 4 <= PI_PRECISION) {
|
||||
r = getPi(Ctor, pr + 4, rm).times(0.25);
|
||||
r.s = x.s;
|
||||
return r;
|
||||
}
|
||||
|
||||
Ctor.precision = wpr = pr + 10;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
// TODO? if (x >= 1 && pr <= PI_PRECISION) atan(x) = halfPi * x.s - atan(1 / x);
|
||||
|
||||
// Argument reduction
|
||||
// Ensure |x| < 0.42
|
||||
// atan(x) = 2 * atan(x / (1 + sqrt(1 + x^2)))
|
||||
|
||||
k = Math.min(28, wpr / LOG_BASE + 2 | 0);
|
||||
|
||||
for (i = k; i; --i) x = x.div(x.times(x).plus(1).sqrt().plus(1));
|
||||
|
||||
external = false;
|
||||
|
||||
j = Math.ceil(wpr / LOG_BASE);
|
||||
n = 1;
|
||||
x2 = x.times(x);
|
||||
r = new Ctor(x);
|
||||
px = x;
|
||||
|
||||
// atan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
|
||||
for (; i !== -1;) {
|
||||
px = px.times(x2);
|
||||
t = r.minus(px.div(n += 2));
|
||||
|
||||
px = px.times(x2);
|
||||
r = t.plus(px.div(n += 2));
|
||||
|
||||
if (r.d[j] !== void 0) for (i = j; r.d[i] === t.d[i] && i--;);
|
||||
}
|
||||
|
||||
if (k) r = r.times(2 << (k - 1));
|
||||
|
||||
external = true;
|
||||
|
||||
return finalise(r, Ctor.precision = pr, Ctor.rounding = rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is a finite number, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isFinite = function () {
|
||||
return !!this.d;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is an integer, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isInteger = P.isInt = function () {
|
||||
return !!this.d && mathfloor(this.e / LOG_BASE) > this.d.length - 2;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is NaN, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isNaN = function () {
|
||||
return !this.s;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is negative, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isNegative = P.isNeg = function () {
|
||||
return this.s < 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is positive, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isPositive = P.isPos = function () {
|
||||
return this.s > 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is 0 or -0, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.isZero = function () {
|
||||
return !!this.d && this.d[0] === 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is less than `y`, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.lessThan = P.lt = function (y) {
|
||||
return this.cmp(y) < 0;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return true if the value of this Decimal is less than or equal to `y`, otherwise return false.
|
||||
*
|
||||
*/
|
||||
P.lessThanOrEqualTo = P.lte = function (y) {
|
||||
return this.cmp(y) < 1;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return the logarithm of the value of this Decimal to the specified base, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* If no base is specified, return log[10](arg).
|
||||
*
|
||||
* log[base](arg) = ln(arg) / ln(base)
|
||||
*
|
||||
* The result will always be correctly rounded if the base of the log is 10, and 'almost always'
|
||||
* otherwise:
|
||||
*
|
||||
* Depending on the rounding mode, the result may be incorrectly rounded if the first fifteen
|
||||
* rounding digits are [49]99999999999999 or [50]00000000000000. In that case, the maximum error
|
||||
* between the result and the correctly rounded result will be one ulp (unit in the last place).
|
||||
*
|
||||
* log[-b](a) = NaN
|
||||
* log[0](a) = NaN
|
||||
* log[1](a) = NaN
|
||||
* log[NaN](a) = NaN
|
||||
* log[Infinity](a) = NaN
|
||||
* log[b](0) = -Infinity
|
||||
* log[b](-0) = -Infinity
|
||||
* log[b](-a) = NaN
|
||||
* log[b](1) = 0
|
||||
* log[b](Infinity) = Infinity
|
||||
* log[b](NaN) = NaN
|
||||
*
|
||||
* [base] {number|string|Decimal} The base of the logarithm.
|
||||
*
|
||||
*/
|
||||
P.logarithm = P.log = function (base) {
|
||||
var isBase10, d, denominator, k, inf, num, sd, r,
|
||||
arg = this,
|
||||
Ctor = arg.constructor,
|
||||
pr = Ctor.precision,
|
||||
rm = Ctor.rounding,
|
||||
guard = 5;
|
||||
|
||||
// Default base is 10.
|
||||
if (base == null) {
|
||||
base = new Ctor(10);
|
||||
isBase10 = true;
|
||||
} else {
|
||||
base = new Ctor(base);
|
||||
d = base.d;
|
||||
|
||||
// Return NaN if base is negative, or non-finite, or is 0 or 1.
|
||||
if (base.s < 0 || !d || !d[0] || base.eq(1)) return new Ctor(NaN);
|
||||
|
||||
isBase10 = base.eq(10);
|
||||
}
|
||||
|
||||
d = arg.d;
|
||||
|
||||
// Is arg negative, non-finite, 0 or 1?
|
||||
if (arg.s < 0 || !d || !d[0] || arg.eq(1)) {
|
||||
return new Ctor(d && !d[0] ? -1 / 0 : arg.s != 1 ? NaN : d ? 0 : 1 / 0);
|
||||
}
|
||||
|
||||
// The result will have a non-terminating decimal expansion if base is 10 and arg is not an
|
||||
// integer power of 10.
|
||||
if (isBase10) {
|
||||
if (d.length > 1) {
|
||||
inf = true;
|
||||
} else {
|
||||
for (k = d[0]; k % 10 === 0;) k /= 10;
|
||||
inf = k !== 1;
|
||||
}
|
||||
}
|
||||
|
||||
external = false;
|
||||
sd = pr + guard;
|
||||
num = naturalLogarithm(arg, sd);
|
||||
denominator = isBase10 ? getLn10(Ctor, sd + 10) : naturalLogarithm(base, sd);
|
||||
|
||||
// The result will have 5 rounding digits.
|
||||
r = divide(num, denominator, sd, 1);
|
||||
|
||||
// If at a rounding boundary, i.e. the result's rounding digits are [49]9999 or [50]0000,
|
||||
// calculate 10 further digits.
|
||||
//
|
||||
// If the result is known to have an infinite decimal expansion, repeat this until it is clear
|
||||
// that the result is above or below the boundary. Otherwise, if after calculating the 10
|
||||
// further digits, the last 14 are nines, round up and assume the result is exact.
|
||||
// Also assume the result is exact if the last 14 are zero.
|
||||
//
|
||||
// Example of a result that will be incorrectly rounded:
|
||||
// log[1048576](4503599627370502) = 2.60000000000000009610279511444746...
|
||||
// The above result correctly rounded using ROUND_CEIL to 1 decimal place should be 2.7, but it
|
||||
// will be given as 2.6 as there are 15 zeros immediately after the requested decimal place, so
|
||||
// the exact result would be assumed to be 2.6, which rounded using ROUND_CEIL to 1 decimal
|
||||
// place is still 2.6.
|
||||
if (checkRoundingDigits(r.d, k = pr, rm)) {
|
||||
|
||||
do {
|
||||
sd += 10;
|
||||
num = naturalLogarithm(arg, sd);
|
||||
denominator = isBase10 ? getLn10(Ctor, sd + 10) : naturalLogarithm(base, sd);
|
||||
r = divide(num, denominator, sd, 1);
|
||||
|
||||
if (!inf) {
|
||||
|
||||
// Check for 14 nines from the 2nd rounding digit, as the first may be 4.
|
||||
if (+digitsToString(r.d).slice(k + 1, k + 15) + 1 == 1e14) {
|
||||
r = finalise(r, pr + 1, 0);
|
||||
}
|
||||
|
||||
break;
|
||||
}
|
||||
} while (checkRoundingDigits(r.d, k += 10, rm));
|
||||
}
|
||||
|
||||
external = true;
|
||||
|
||||
return finalise(r, pr, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the maximum of the arguments and the value of this Decimal.
|
||||
*
|
||||
* arguments {number|string|Decimal}
|
||||
*
|
||||
P.max = function () {
|
||||
Array.prototype.push.call(arguments, this);
|
||||
return maxOrMin(this.constructor, arguments, 'lt');
|
||||
};
|
||||
*/
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the minimum of the arguments and the value of this Decimal.
|
||||
*
|
||||
* arguments {number|string|Decimal}
|
||||
*
|
||||
P.min = function () {
|
||||
Array.prototype.push.call(arguments, this);
|
||||
return maxOrMin(this.constructor, arguments, 'gt');
|
||||
};
|
||||
*/
|
||||
|
||||
|
||||
/*
|
||||
* n - 0 = n
|
||||
* n - N = N
|
||||
* n - I = -I
|
||||
* 0 - n = -n
|
||||
* 0 - 0 = 0
|
||||
* 0 - N = N
|
||||
* 0 - I = -I
|
||||
* N - n = N
|
||||
* N - 0 = N
|
||||
* N - N = N
|
||||
* N - I = N
|
||||
* I - n = I
|
||||
* I - 0 = I
|
||||
* I - N = N
|
||||
* I - I = N
|
||||
*
|
||||
* Return a new Decimal whose value is the value of this Decimal minus `y`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.minus = P.sub = function (y) {
|
||||
var d, e, i, j, k, len, pr, rm, xd, xe, xLTy, yd,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
y = new Ctor(y);
|
||||
|
||||
// If either is not finite...
|
||||
if (!x.d || !y.d) {
|
||||
|
||||
// Return NaN if either is NaN.
|
||||
if (!x.s || !y.s) y = new Ctor(NaN);
|
||||
|
||||
// Return y negated if x is finite and y is ±Infinity.
|
||||
else if (x.d) y.s = -y.s;
|
||||
|
||||
// Return x if y is finite and x is ±Infinity.
|
||||
// Return x if both are ±Infinity with different signs.
|
||||
// Return NaN if both are ±Infinity with the same sign.
|
||||
else y = new Ctor(y.d || x.s !== y.s ? x : NaN);
|
||||
|
||||
return y;
|
||||
}
|
||||
|
||||
// If signs differ...
|
||||
if (x.s != y.s) {
|
||||
y.s = -y.s;
|
||||
return x.plus(y);
|
||||
}
|
||||
|
||||
xd = x.d;
|
||||
yd = y.d;
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
|
||||
// If either is zero...
|
||||
if (!xd[0] || !yd[0]) {
|
||||
|
||||
// Return y negated if x is zero and y is non-zero.
|
||||
if (yd[0]) y.s = -y.s;
|
||||
|
||||
// Return x if y is zero and x is non-zero.
|
||||
else if (xd[0]) y = new Ctor(x);
|
||||
|
||||
// Return zero if both are zero.
|
||||
// From IEEE 754 (2008) 6.3: 0 - 0 = -0 - -0 = -0 when rounding to -Infinity.
|
||||
else return new Ctor(rm === 3 ? -0 : 0);
|
||||
|
||||
return external ? finalise(y, pr, rm) : y;
|
||||
}
|
||||
|
||||
// x and y are finite, non-zero numbers with the same sign.
|
||||
|
||||
// Calculate base 1e7 exponents.
|
||||
e = mathfloor(y.e / LOG_BASE);
|
||||
xe = mathfloor(x.e / LOG_BASE);
|
||||
|
||||
xd = xd.slice();
|
||||
k = xe - e;
|
||||
|
||||
// If base 1e7 exponents differ...
|
||||
if (k) {
|
||||
xLTy = k < 0;
|
||||
|
||||
if (xLTy) {
|
||||
d = xd;
|
||||
k = -k;
|
||||
len = yd.length;
|
||||
} else {
|
||||
d = yd;
|
||||
e = xe;
|
||||
len = xd.length;
|
||||
}
|
||||
|
||||
// Numbers with massively different exponents would result in a very high number of
|
||||
// zeros needing to be prepended, but this can be avoided while still ensuring correct
|
||||
// rounding by limiting the number of zeros to `Math.ceil(pr / LOG_BASE) + 2`.
|
||||
i = Math.max(Math.ceil(pr / LOG_BASE), len) + 2;
|
||||
|
||||
if (k > i) {
|
||||
k = i;
|
||||
d.length = 1;
|
||||
}
|
||||
|
||||
// Prepend zeros to equalise exponents.
|
||||
d.reverse();
|
||||
for (i = k; i--;) d.push(0);
|
||||
d.reverse();
|
||||
|
||||
// Base 1e7 exponents equal.
|
||||
} else {
|
||||
|
||||
// Check digits to determine which is the bigger number.
|
||||
|
||||
i = xd.length;
|
||||
len = yd.length;
|
||||
xLTy = i < len;
|
||||
if (xLTy) len = i;
|
||||
|
||||
for (i = 0; i < len; i++) {
|
||||
if (xd[i] != yd[i]) {
|
||||
xLTy = xd[i] < yd[i];
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
k = 0;
|
||||
}
|
||||
|
||||
if (xLTy) {
|
||||
d = xd;
|
||||
xd = yd;
|
||||
yd = d;
|
||||
y.s = -y.s;
|
||||
}
|
||||
|
||||
len = xd.length;
|
||||
|
||||
// Append zeros to `xd` if shorter.
|
||||
// Don't add zeros to `yd` if shorter as subtraction only needs to start at `yd` length.
|
||||
for (i = yd.length - len; i > 0; --i) xd[len++] = 0;
|
||||
|
||||
// Subtract yd from xd.
|
||||
for (i = yd.length; i > k;) {
|
||||
|
||||
if (xd[--i] < yd[i]) {
|
||||
for (j = i; j && xd[--j] === 0;) xd[j] = BASE - 1;
|
||||
--xd[j];
|
||||
xd[i] += BASE;
|
||||
}
|
||||
|
||||
xd[i] -= yd[i];
|
||||
}
|
||||
|
||||
// Remove trailing zeros.
|
||||
for (; xd[--len] === 0;) xd.pop();
|
||||
|
||||
// Remove leading zeros and adjust exponent accordingly.
|
||||
for (; xd[0] === 0; xd.shift()) --e;
|
||||
|
||||
// Zero?
|
||||
if (!xd[0]) return new Ctor(rm === 3 ? -0 : 0);
|
||||
|
||||
y.d = xd;
|
||||
y.e = getBase10Exponent(xd, e);
|
||||
|
||||
return external ? finalise(y, pr, rm) : y;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* n % 0 = N
|
||||
* n % N = N
|
||||
* n % I = n
|
||||
* 0 % n = 0
|
||||
* -0 % n = -0
|
||||
* 0 % 0 = N
|
||||
* 0 % N = N
|
||||
* 0 % I = 0
|
||||
* N % n = N
|
||||
* N % 0 = N
|
||||
* N % N = N
|
||||
* N % I = N
|
||||
* I % n = N
|
||||
* I % 0 = N
|
||||
* I % N = N
|
||||
* I % I = N
|
||||
*
|
||||
* Return a new Decimal whose value is the value of this Decimal modulo `y`, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* The result depends on the modulo mode.
|
||||
*
|
||||
*/
|
||||
P.modulo = P.mod = function (y) {
|
||||
var q,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
y = new Ctor(y);
|
||||
|
||||
// Return NaN if x is ±Infinity or NaN, or y is NaN or ±0.
|
||||
if (!x.d || !y.s || y.d && !y.d[0]) return new Ctor(NaN);
|
||||
|
||||
// Return x if y is ±Infinity or x is ±0.
|
||||
if (!y.d || x.d && !x.d[0]) {
|
||||
return finalise(new Ctor(x), Ctor.precision, Ctor.rounding);
|
||||
}
|
||||
|
||||
// Prevent rounding of intermediate calculations.
|
||||
external = false;
|
||||
|
||||
if (Ctor.modulo == 9) {
|
||||
|
||||
// Euclidian division: q = sign(y) * floor(x / abs(y))
|
||||
// result = x - q * y where 0 <= result < abs(y)
|
||||
q = divide(x, y.abs(), 0, 3, 1);
|
||||
q.s *= y.s;
|
||||
} else {
|
||||
q = divide(x, y, 0, Ctor.modulo, 1);
|
||||
}
|
||||
|
||||
q = q.times(y);
|
||||
|
||||
external = true;
|
||||
|
||||
return x.minus(q);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural exponential of the value of this Decimal,
|
||||
* i.e. the base e raised to the power the value of this Decimal, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.naturalExponential = P.exp = function () {
|
||||
return naturalExponential(this);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural logarithm of the value of this Decimal,
|
||||
* rounded to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.naturalLogarithm = P.ln = function () {
|
||||
return naturalLogarithm(this);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal negated, i.e. as if multiplied by
|
||||
* -1.
|
||||
*
|
||||
*/
|
||||
P.negated = P.neg = function () {
|
||||
var x = new this.constructor(this);
|
||||
x.s = -x.s;
|
||||
return finalise(x);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* n + 0 = n
|
||||
* n + N = N
|
||||
* n + I = I
|
||||
* 0 + n = n
|
||||
* 0 + 0 = 0
|
||||
* 0 + N = N
|
||||
* 0 + I = I
|
||||
* N + n = N
|
||||
* N + 0 = N
|
||||
* N + N = N
|
||||
* N + I = N
|
||||
* I + n = I
|
||||
* I + 0 = I
|
||||
* I + N = N
|
||||
* I + I = I
|
||||
*
|
||||
* Return a new Decimal whose value is the value of this Decimal plus `y`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.plus = P.add = function (y) {
|
||||
var carry, d, e, i, k, len, pr, rm, xd, yd,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
y = new Ctor(y);
|
||||
|
||||
// If either is not finite...
|
||||
if (!x.d || !y.d) {
|
||||
|
||||
// Return NaN if either is NaN.
|
||||
if (!x.s || !y.s) y = new Ctor(NaN);
|
||||
|
||||
// Return x if y is finite and x is ±Infinity.
|
||||
// Return x if both are ±Infinity with the same sign.
|
||||
// Return NaN if both are ±Infinity with different signs.
|
||||
// Return y if x is finite and y is ±Infinity.
|
||||
else if (!x.d) y = new Ctor(y.d || x.s === y.s ? x : NaN);
|
||||
|
||||
return y;
|
||||
}
|
||||
|
||||
// If signs differ...
|
||||
if (x.s != y.s) {
|
||||
y.s = -y.s;
|
||||
return x.minus(y);
|
||||
}
|
||||
|
||||
xd = x.d;
|
||||
yd = y.d;
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
|
||||
// If either is zero...
|
||||
if (!xd[0] || !yd[0]) {
|
||||
|
||||
// Return x if y is zero.
|
||||
// Return y if y is non-zero.
|
||||
if (!yd[0]) y = new Ctor(x);
|
||||
|
||||
return external ? finalise(y, pr, rm) : y;
|
||||
}
|
||||
|
||||
// x and y are finite, non-zero numbers with the same sign.
|
||||
|
||||
// Calculate base 1e7 exponents.
|
||||
k = mathfloor(x.e / LOG_BASE);
|
||||
e = mathfloor(y.e / LOG_BASE);
|
||||
|
||||
xd = xd.slice();
|
||||
i = k - e;
|
||||
|
||||
// If base 1e7 exponents differ...
|
||||
if (i) {
|
||||
|
||||
if (i < 0) {
|
||||
d = xd;
|
||||
i = -i;
|
||||
len = yd.length;
|
||||
} else {
|
||||
d = yd;
|
||||
e = k;
|
||||
len = xd.length;
|
||||
}
|
||||
|
||||
// Limit number of zeros prepended to max(ceil(pr / LOG_BASE), len) + 1.
|
||||
k = Math.ceil(pr / LOG_BASE);
|
||||
len = k > len ? k + 1 : len + 1;
|
||||
|
||||
if (i > len) {
|
||||
i = len;
|
||||
d.length = 1;
|
||||
}
|
||||
|
||||
// Prepend zeros to equalise exponents. Note: Faster to use reverse then do unshifts.
|
||||
d.reverse();
|
||||
for (; i--;) d.push(0);
|
||||
d.reverse();
|
||||
}
|
||||
|
||||
len = xd.length;
|
||||
i = yd.length;
|
||||
|
||||
// If yd is longer than xd, swap xd and yd so xd points to the longer array.
|
||||
if (len - i < 0) {
|
||||
i = len;
|
||||
d = yd;
|
||||
yd = xd;
|
||||
xd = d;
|
||||
}
|
||||
|
||||
// Only start adding at yd.length - 1 as the further digits of xd can be left as they are.
|
||||
for (carry = 0; i;) {
|
||||
carry = (xd[--i] = xd[i] + yd[i] + carry) / BASE | 0;
|
||||
xd[i] %= BASE;
|
||||
}
|
||||
|
||||
if (carry) {
|
||||
xd.unshift(carry);
|
||||
++e;
|
||||
}
|
||||
|
||||
// Remove trailing zeros.
|
||||
// No need to check for zero, as +x + +y != 0 && -x + -y != 0
|
||||
for (len = xd.length; xd[--len] == 0;) xd.pop();
|
||||
|
||||
y.d = xd;
|
||||
y.e = getBase10Exponent(xd, e);
|
||||
|
||||
return external ? finalise(y, pr, rm) : y;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return the number of significant digits of the value of this Decimal.
|
||||
*
|
||||
* [z] {boolean|number} Whether to count integer-part trailing zeros: true, false, 1 or 0.
|
||||
*
|
||||
*/
|
||||
P.precision = P.sd = function (z) {
|
||||
var k,
|
||||
x = this;
|
||||
|
||||
if (z !== void 0 && z !== !!z && z !== 1 && z !== 0) throw Error(invalidArgument + z);
|
||||
|
||||
if (x.d) {
|
||||
k = getPrecision(x.d);
|
||||
if (z && x.e + 1 > k) k = x.e + 1;
|
||||
} else {
|
||||
k = NaN;
|
||||
}
|
||||
|
||||
return k;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal rounded to a whole number using
|
||||
* rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.round = function () {
|
||||
var x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
return finalise(new Ctor(x), x.e + 1, Ctor.rounding);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the sine of the value in radians of this Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-1, 1]
|
||||
*
|
||||
* sin(x) = x - x^3/3! + x^5/5! - ...
|
||||
*
|
||||
* sin(0) = 0
|
||||
* sin(-0) = -0
|
||||
* sin(Infinity) = NaN
|
||||
* sin(-Infinity) = NaN
|
||||
* sin(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.sine = P.sin = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite()) return new Ctor(NaN);
|
||||
if (x.isZero()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + Math.max(x.e, x.sd()) + LOG_BASE;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = sine(Ctor, toLessThanHalfPi(Ctor, x));
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return finalise(quadrant > 2 ? x.neg() : x, pr, rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the square root of this Decimal, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* sqrt(-n) = N
|
||||
* sqrt(N) = N
|
||||
* sqrt(-I) = N
|
||||
* sqrt(I) = I
|
||||
* sqrt(0) = 0
|
||||
* sqrt(-0) = -0
|
||||
*
|
||||
*/
|
||||
P.squareRoot = P.sqrt = function () {
|
||||
var m, n, sd, r, rep, t,
|
||||
x = this,
|
||||
d = x.d,
|
||||
e = x.e,
|
||||
s = x.s,
|
||||
Ctor = x.constructor;
|
||||
|
||||
// Negative/NaN/Infinity/zero?
|
||||
if (s !== 1 || !d || !d[0]) {
|
||||
return new Ctor(!s || s < 0 && (!d || d[0]) ? NaN : d ? x : 1 / 0);
|
||||
}
|
||||
|
||||
external = false;
|
||||
|
||||
// Initial estimate.
|
||||
s = Math.sqrt(+x);
|
||||
|
||||
// Math.sqrt underflow/overflow?
|
||||
// Pass x to Math.sqrt as integer, then adjust the exponent of the result.
|
||||
if (s == 0 || s == 1 / 0) {
|
||||
n = digitsToString(d);
|
||||
|
||||
if ((n.length + e) % 2 == 0) n += '0';
|
||||
s = Math.sqrt(n);
|
||||
e = mathfloor((e + 1) / 2) - (e < 0 || e % 2);
|
||||
|
||||
if (s == 1 / 0) {
|
||||
n = '1e' + e;
|
||||
} else {
|
||||
n = s.toExponential();
|
||||
n = n.slice(0, n.indexOf('e') + 1) + e;
|
||||
}
|
||||
|
||||
r = new Ctor(n);
|
||||
} else {
|
||||
r = new Ctor(s.toString());
|
||||
}
|
||||
|
||||
sd = (e = Ctor.precision) + 3;
|
||||
|
||||
// Newton-Raphson iteration.
|
||||
for (;;) {
|
||||
t = r;
|
||||
r = t.plus(divide(x, t, sd + 2, 1)).times(0.5);
|
||||
|
||||
// TODO? Replace with for-loop and checkRoundingDigits.
|
||||
if (digitsToString(t.d).slice(0, sd) === (n = digitsToString(r.d)).slice(0, sd)) {
|
||||
n = n.slice(sd - 3, sd + 1);
|
||||
|
||||
// The 4th rounding digit may be in error by -1 so if the 4 rounding digits are 9999 or
|
||||
// 4999, i.e. approaching a rounding boundary, continue the iteration.
|
||||
if (n == '9999' || !rep && n == '4999') {
|
||||
|
||||
// On the first iteration only, check to see if rounding up gives the exact result as the
|
||||
// nines may infinitely repeat.
|
||||
if (!rep) {
|
||||
finalise(t, e + 1, 0);
|
||||
|
||||
if (t.times(t).eq(x)) {
|
||||
r = t;
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
sd += 4;
|
||||
rep = 1;
|
||||
} else {
|
||||
|
||||
// If the rounding digits are null, 0{0,4} or 50{0,3}, check for an exact result.
|
||||
// If not, then there are further digits and m will be truthy.
|
||||
if (!+n || !+n.slice(1) && n.charAt(0) == '5') {
|
||||
|
||||
// Truncate to the first rounding digit.
|
||||
finalise(r, e + 1, 1);
|
||||
m = !r.times(r).eq(x);
|
||||
}
|
||||
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
external = true;
|
||||
|
||||
return finalise(r, e, Ctor.rounding, m);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the tangent of the value in radians of this Decimal.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-Infinity, Infinity]
|
||||
*
|
||||
* tan(0) = 0
|
||||
* tan(-0) = -0
|
||||
* tan(Infinity) = NaN
|
||||
* tan(-Infinity) = NaN
|
||||
* tan(NaN) = NaN
|
||||
*
|
||||
*/
|
||||
P.tangent = P.tan = function () {
|
||||
var pr, rm,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!x.isFinite()) return new Ctor(NaN);
|
||||
if (x.isZero()) return new Ctor(x);
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
Ctor.precision = pr + 10;
|
||||
Ctor.rounding = 1;
|
||||
|
||||
x = x.sin();
|
||||
x.s = 1;
|
||||
x = divide(x, new Ctor(1).minus(x.times(x)).sqrt(), pr + 10, 0);
|
||||
|
||||
Ctor.precision = pr;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return finalise(quadrant == 2 || quadrant == 4 ? x.neg() : x, pr, rm, true);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* n * 0 = 0
|
||||
* n * N = N
|
||||
* n * I = I
|
||||
* 0 * n = 0
|
||||
* 0 * 0 = 0
|
||||
* 0 * N = N
|
||||
* 0 * I = N
|
||||
* N * n = N
|
||||
* N * 0 = N
|
||||
* N * N = N
|
||||
* N * I = N
|
||||
* I * n = I
|
||||
* I * 0 = N
|
||||
* I * N = N
|
||||
* I * I = I
|
||||
*
|
||||
* Return a new Decimal whose value is this Decimal times `y`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
*/
|
||||
P.times = P.mul = function (y) {
|
||||
var carry, e, i, k, r, rL, t, xdL, ydL,
|
||||
x = this,
|
||||
Ctor = x.constructor,
|
||||
xd = x.d,
|
||||
yd = (y = new Ctor(y)).d;
|
||||
|
||||
y.s *= x.s;
|
||||
|
||||
// If either is NaN, ±Infinity or ±0...
|
||||
if (!xd || !xd[0] || !yd || !yd[0]) {
|
||||
|
||||
return new Ctor(!y.s || xd && !xd[0] && !yd || yd && !yd[0] && !xd
|
||||
|
||||
// Return NaN if either is NaN.
|
||||
// Return NaN if x is ±0 and y is ±Infinity, or y is ±0 and x is ±Infinity.
|
||||
? NaN
|
||||
|
||||
// Return ±Infinity if either is ±Infinity.
|
||||
// Return ±0 if either is ±0.
|
||||
: !xd || !yd ? y.s / 0 : y.s * 0);
|
||||
}
|
||||
|
||||
e = mathfloor(x.e / LOG_BASE) + mathfloor(y.e / LOG_BASE);
|
||||
xdL = xd.length;
|
||||
ydL = yd.length;
|
||||
|
||||
// Ensure xd points to the longer array.
|
||||
if (xdL < ydL) {
|
||||
r = xd;
|
||||
xd = yd;
|
||||
yd = r;
|
||||
rL = xdL;
|
||||
xdL = ydL;
|
||||
ydL = rL;
|
||||
}
|
||||
|
||||
// Initialise the result array with zeros.
|
||||
r = [];
|
||||
rL = xdL + ydL;
|
||||
for (i = rL; i--;) r.push(0);
|
||||
|
||||
// Multiply!
|
||||
for (i = ydL; --i >= 0;) {
|
||||
carry = 0;
|
||||
for (k = xdL + i; k > i;) {
|
||||
t = r[k] + yd[i] * xd[k - i - 1] + carry;
|
||||
r[k--] = t % BASE | 0;
|
||||
carry = t / BASE | 0;
|
||||
}
|
||||
|
||||
r[k] = (r[k] + carry) % BASE | 0;
|
||||
}
|
||||
|
||||
// Remove trailing zeros.
|
||||
for (; !r[--rL];) r.pop();
|
||||
|
||||
if (carry) ++e;
|
||||
else r.shift();
|
||||
|
||||
y.d = r;
|
||||
y.e = getBase10Exponent(r, e);
|
||||
|
||||
return external ? finalise(y, Ctor.precision, Ctor.rounding) : y;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal in base 2, round to `sd` significant
|
||||
* digits using rounding mode `rm`.
|
||||
*
|
||||
* If the optional `sd` argument is present then return binary exponential notation.
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 1 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toBinary = function (sd, rm) {
|
||||
return toStringBinary(this, 2, sd, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal rounded to a maximum of `dp`
|
||||
* decimal places using rounding mode `rm` or `rounding` if `rm` is omitted.
|
||||
*
|
||||
* If `dp` is omitted, return a new Decimal whose value is the value of this Decimal.
|
||||
*
|
||||
* [dp] {number} Decimal places. Integer, 0 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toDecimalPlaces = P.toDP = function (dp, rm) {
|
||||
var x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
x = new Ctor(x);
|
||||
if (dp === void 0) return x;
|
||||
|
||||
checkInt32(dp, 0, MAX_DIGITS);
|
||||
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
|
||||
return finalise(x, dp + x.e + 1, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal in exponential notation rounded to
|
||||
* `dp` fixed decimal places using rounding mode `rounding`.
|
||||
*
|
||||
* [dp] {number} Decimal places. Integer, 0 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toExponential = function (dp, rm) {
|
||||
var str,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (dp === void 0) {
|
||||
str = finiteToString(x, true);
|
||||
} else {
|
||||
checkInt32(dp, 0, MAX_DIGITS);
|
||||
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
|
||||
x = finalise(new Ctor(x), dp + 1, rm);
|
||||
str = finiteToString(x, true, dp + 1);
|
||||
}
|
||||
|
||||
return x.isNeg() && !x.isZero() ? '-' + str : str;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal in normal (fixed-point) notation to
|
||||
* `dp` fixed decimal places and rounded using rounding mode `rm` or `rounding` if `rm` is
|
||||
* omitted.
|
||||
*
|
||||
* As with JavaScript numbers, (-0).toFixed(0) is '0', but e.g. (-0.00001).toFixed(0) is '-0'.
|
||||
*
|
||||
* [dp] {number} Decimal places. Integer, 0 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
* (-0).toFixed(0) is '0', but (-0.1).toFixed(0) is '-0'.
|
||||
* (-0).toFixed(1) is '0.0', but (-0.01).toFixed(1) is '-0.0'.
|
||||
* (-0).toFixed(3) is '0.000'.
|
||||
* (-0.5).toFixed(0) is '-0'.
|
||||
*
|
||||
*/
|
||||
P.toFixed = function (dp, rm) {
|
||||
var str, y,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (dp === void 0) {
|
||||
str = finiteToString(x);
|
||||
} else {
|
||||
checkInt32(dp, 0, MAX_DIGITS);
|
||||
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
|
||||
y = finalise(new Ctor(x), dp + x.e + 1, rm);
|
||||
str = finiteToString(y, false, dp + y.e + 1);
|
||||
}
|
||||
|
||||
// To determine whether to add the minus sign look at the value before it was rounded,
|
||||
// i.e. look at `x` rather than `y`.
|
||||
return x.isNeg() && !x.isZero() ? '-' + str : str;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return an array representing the value of this Decimal as a simple fraction with an integer
|
||||
* numerator and an integer denominator.
|
||||
*
|
||||
* The denominator will be a positive non-zero value less than or equal to the specified maximum
|
||||
* denominator. If a maximum denominator is not specified, the denominator will be the lowest
|
||||
* value necessary to represent the number exactly.
|
||||
*
|
||||
* [maxD] {number|string|Decimal} Maximum denominator. Integer >= 1 and < Infinity.
|
||||
*
|
||||
*/
|
||||
P.toFraction = function (maxD) {
|
||||
var d, d0, d1, d2, e, k, n, n0, n1, pr, q, r,
|
||||
x = this,
|
||||
xd = x.d,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (!xd) return new Ctor(x);
|
||||
|
||||
n1 = d0 = new Ctor(1);
|
||||
d1 = n0 = new Ctor(0);
|
||||
|
||||
d = new Ctor(d1);
|
||||
e = d.e = getPrecision(xd) - x.e - 1;
|
||||
k = e % LOG_BASE;
|
||||
d.d[0] = mathpow(10, k < 0 ? LOG_BASE + k : k);
|
||||
|
||||
if (maxD == null) {
|
||||
|
||||
// d is 10**e, the minimum max-denominator needed.
|
||||
maxD = e > 0 ? d : n1;
|
||||
} else {
|
||||
n = new Ctor(maxD);
|
||||
if (!n.isInt() || n.lt(n1)) throw Error(invalidArgument + n);
|
||||
maxD = n.gt(d) ? (e > 0 ? d : n1) : n;
|
||||
}
|
||||
|
||||
external = false;
|
||||
n = new Ctor(digitsToString(xd));
|
||||
pr = Ctor.precision;
|
||||
Ctor.precision = e = xd.length * LOG_BASE * 2;
|
||||
|
||||
for (;;) {
|
||||
q = divide(n, d, 0, 1, 1);
|
||||
d2 = d0.plus(q.times(d1));
|
||||
if (d2.cmp(maxD) == 1) break;
|
||||
d0 = d1;
|
||||
d1 = d2;
|
||||
d2 = n1;
|
||||
n1 = n0.plus(q.times(d2));
|
||||
n0 = d2;
|
||||
d2 = d;
|
||||
d = n.minus(q.times(d2));
|
||||
n = d2;
|
||||
}
|
||||
|
||||
d2 = divide(maxD.minus(d0), d1, 0, 1, 1);
|
||||
n0 = n0.plus(d2.times(n1));
|
||||
d0 = d0.plus(d2.times(d1));
|
||||
n0.s = n1.s = x.s;
|
||||
|
||||
// Determine which fraction is closer to x, n0/d0 or n1/d1?
|
||||
r = divide(n1, d1, e, 1).minus(x).abs().cmp(divide(n0, d0, e, 1).minus(x).abs()) < 1
|
||||
? [n1, d1] : [n0, d0];
|
||||
|
||||
Ctor.precision = pr;
|
||||
external = true;
|
||||
|
||||
return r;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal in base 16, round to `sd` significant
|
||||
* digits using rounding mode `rm`.
|
||||
*
|
||||
* If the optional `sd` argument is present then return binary exponential notation.
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 1 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toHexadecimal = P.toHex = function (sd, rm) {
|
||||
return toStringBinary(this, 16, sd, rm);
|
||||
};
|
||||
|
||||
|
||||
|
||||
/*
|
||||
* Returns a new Decimal whose value is the nearest multiple of the magnitude of `y` to the value
|
||||
* of this Decimal.
|
||||
*
|
||||
* If the value of this Decimal is equidistant from two multiples of `y`, the rounding mode `rm`,
|
||||
* or `Decimal.rounding` if `rm` is omitted, determines the direction of the nearest multiple.
|
||||
*
|
||||
* In the context of this method, rounding mode 4 (ROUND_HALF_UP) is the same as rounding mode 0
|
||||
* (ROUND_UP), and so on.
|
||||
*
|
||||
* The return value will always have the same sign as this Decimal, unless either this Decimal
|
||||
* or `y` is NaN, in which case the return value will be also be NaN.
|
||||
*
|
||||
* The return value is not affected by the value of `precision`.
|
||||
*
|
||||
* y {number|string|Decimal} The magnitude to round to a multiple of.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
* 'toNearest() rounding mode not an integer: {rm}'
|
||||
* 'toNearest() rounding mode out of range: {rm}'
|
||||
*
|
||||
*/
|
||||
P.toNearest = function (y, rm) {
|
||||
var x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
x = new Ctor(x);
|
||||
|
||||
if (y == null) {
|
||||
|
||||
// If x is not finite, return x.
|
||||
if (!x.d) return x;
|
||||
|
||||
y = new Ctor(1);
|
||||
rm = Ctor.rounding;
|
||||
} else {
|
||||
y = new Ctor(y);
|
||||
if (rm !== void 0) checkInt32(rm, 0, 8);
|
||||
|
||||
// If x is not finite, return x if y is not NaN, else NaN.
|
||||
if (!x.d) return y.s ? x : y;
|
||||
|
||||
// If y is not finite, return Infinity with the sign of x if y is Infinity, else NaN.
|
||||
if (!y.d) {
|
||||
if (y.s) y.s = x.s;
|
||||
return y;
|
||||
}
|
||||
}
|
||||
|
||||
// If y is not zero, calculate the nearest multiple of y to x.
|
||||
if (y.d[0]) {
|
||||
external = false;
|
||||
if (rm < 4) rm = [4, 5, 7, 8][rm];
|
||||
x = divide(x, y, 0, rm, 1).times(y);
|
||||
external = true;
|
||||
finalise(x);
|
||||
|
||||
// If y is zero, return zero with the sign of x.
|
||||
} else {
|
||||
y.s = x.s;
|
||||
x = y;
|
||||
}
|
||||
|
||||
return x;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return the value of this Decimal converted to a number primitive.
|
||||
* Zero keeps its sign.
|
||||
*
|
||||
*/
|
||||
P.toNumber = function () {
|
||||
return +this;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal in base 8, round to `sd` significant
|
||||
* digits using rounding mode `rm`.
|
||||
*
|
||||
* If the optional `sd` argument is present then return binary exponential notation.
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 1 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toOctal = function (sd, rm) {
|
||||
return toStringBinary(this, 8, sd, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal raised to the power `y`, rounded
|
||||
* to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* ECMAScript compliant.
|
||||
*
|
||||
* pow(x, NaN) = NaN
|
||||
* pow(x, ±0) = 1
|
||||
|
||||
* pow(NaN, non-zero) = NaN
|
||||
* pow(abs(x) > 1, +Infinity) = +Infinity
|
||||
* pow(abs(x) > 1, -Infinity) = +0
|
||||
* pow(abs(x) == 1, ±Infinity) = NaN
|
||||
* pow(abs(x) < 1, +Infinity) = +0
|
||||
* pow(abs(x) < 1, -Infinity) = +Infinity
|
||||
* pow(+Infinity, y > 0) = +Infinity
|
||||
* pow(+Infinity, y < 0) = +0
|
||||
* pow(-Infinity, odd integer > 0) = -Infinity
|
||||
* pow(-Infinity, even integer > 0) = +Infinity
|
||||
* pow(-Infinity, odd integer < 0) = -0
|
||||
* pow(-Infinity, even integer < 0) = +0
|
||||
* pow(+0, y > 0) = +0
|
||||
* pow(+0, y < 0) = +Infinity
|
||||
* pow(-0, odd integer > 0) = -0
|
||||
* pow(-0, even integer > 0) = +0
|
||||
* pow(-0, odd integer < 0) = -Infinity
|
||||
* pow(-0, even integer < 0) = +Infinity
|
||||
* pow(finite x < 0, finite non-integer) = NaN
|
||||
*
|
||||
* For non-integer or very large exponents pow(x, y) is calculated using
|
||||
*
|
||||
* x^y = exp(y*ln(x))
|
||||
*
|
||||
* Assuming the first 15 rounding digits are each equally likely to be any digit 0-9, the
|
||||
* probability of an incorrectly rounded result
|
||||
* P([49]9{14} | [50]0{14}) = 2 * 0.2 * 10^-14 = 4e-15 = 1/2.5e+14
|
||||
* i.e. 1 in 250,000,000,000,000
|
||||
*
|
||||
* If a result is incorrectly rounded the maximum error will be 1 ulp (unit in last place).
|
||||
*
|
||||
* y {number|string|Decimal} The power to which to raise this Decimal.
|
||||
*
|
||||
*/
|
||||
P.toPower = P.pow = function (y) {
|
||||
var e, k, pr, r, rm, sign, yIsInt,
|
||||
x = this,
|
||||
Ctor = x.constructor,
|
||||
yn = +(y = new Ctor(y));
|
||||
|
||||
// Either ±Infinity, NaN or ±0?
|
||||
if (!x.d || !y.d || !x.d[0] || !y.d[0]) return new Ctor(mathpow(+x, yn));
|
||||
|
||||
x = new Ctor(x);
|
||||
|
||||
if (x.eq(1)) return x;
|
||||
|
||||
pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
|
||||
if (y.eq(1)) return finalise(x, pr, rm);
|
||||
|
||||
e = mathfloor(y.e / LOG_BASE);
|
||||
k = y.d.length - 1;
|
||||
yIsInt = e >= k;
|
||||
sign = x.s;
|
||||
|
||||
if (!yIsInt) {
|
||||
if (sign < 0) return new Ctor(NaN);
|
||||
|
||||
// If y is a small integer use the 'exponentiation by squaring' algorithm.
|
||||
} else if ((k = yn < 0 ? -yn : yn) <= MAX_SAFE_INTEGER) {
|
||||
r = intPow(Ctor, x, k, pr);
|
||||
return y.s < 0 ? new Ctor(1).div(r) : finalise(r, pr, rm);
|
||||
}
|
||||
|
||||
// Result is negative if x is negative and the last digit of integer y is odd.
|
||||
sign = sign < 0 && y.d[Math.max(e, k)] & 1 ? -1 : 1;
|
||||
|
||||
// Estimate result exponent.
|
||||
// x^y = 10^e, where e = y * log10(x)
|
||||
// log10(x) = log10(x_significand) + x_exponent
|
||||
// log10(x_significand) = ln(x_significand) / ln(10)
|
||||
k = mathpow(+x, yn);
|
||||
e = k == 0 || !isFinite(k)
|
||||
? mathfloor(yn * (Math.log('0.' + digitsToString(x.d)) / Math.LN10 + x.e + 1))
|
||||
: new Ctor(k + '').e;
|
||||
|
||||
// Estimate may be incorrect e.g. x: 0.999999999999999999, y: 2.29, e: 0, r.e: -1.
|
||||
|
||||
// Overflow/underflow?
|
||||
if (e > Ctor.maxE + 1 || e < Ctor.minE - 1) return new Ctor(e > 0 ? sign / 0 : 0);
|
||||
|
||||
external = false;
|
||||
Ctor.rounding = x.s = 1;
|
||||
|
||||
// Estimate the extra guard digits needed to ensure five correct rounding digits from
|
||||
// naturalLogarithm(x). Example of failure without these extra digits (precision: 10):
|
||||
// new Decimal(2.32456).pow('2087987436534566.46411')
|
||||
// should be 1.162377823e+764914905173815, but is 1.162355823e+764914905173815
|
||||
k = Math.min(12, (e + '').length);
|
||||
|
||||
// r = x^y = exp(y*ln(x))
|
||||
r = naturalExponential(y.times(naturalLogarithm(x, pr + k)), pr);
|
||||
|
||||
// Truncate to the required precision plus five rounding digits.
|
||||
r = finalise(r, pr + 5, 1);
|
||||
|
||||
// If the rounding digits are [49]9999 or [50]0000 increase the precision by 10 and recalculate
|
||||
// the result.
|
||||
if (checkRoundingDigits(r.d, pr, rm)) {
|
||||
e = pr + 10;
|
||||
|
||||
// Truncate to the increased precision plus five rounding digits.
|
||||
r = finalise(naturalExponential(y.times(naturalLogarithm(x, e + k)), e), e + 5, 1);
|
||||
|
||||
// Check for 14 nines from the 2nd rounding digit (the first rounding digit may be 4 or 9).
|
||||
if (+digitsToString(r.d).slice(pr + 1, pr + 15) + 1 == 1e14) {
|
||||
r = finalise(r, pr + 1, 0);
|
||||
}
|
||||
}
|
||||
|
||||
r.s = sign;
|
||||
external = true;
|
||||
Ctor.rounding = rm;
|
||||
|
||||
return finalise(r, pr, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal rounded to `sd` significant digits
|
||||
* using rounding mode `rounding`.
|
||||
*
|
||||
* Return exponential notation if `sd` is less than the number of digits necessary to represent
|
||||
* the integer part of the value in normal notation.
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 1 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
*/
|
||||
P.toPrecision = function (sd, rm) {
|
||||
var str,
|
||||
x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (sd === void 0) {
|
||||
str = finiteToString(x, x.e <= Ctor.toExpNeg || x.e >= Ctor.toExpPos);
|
||||
} else {
|
||||
checkInt32(sd, 1, MAX_DIGITS);
|
||||
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
|
||||
x = finalise(new Ctor(x), sd, rm);
|
||||
str = finiteToString(x, sd <= x.e || x.e <= Ctor.toExpNeg, sd);
|
||||
}
|
||||
|
||||
return x.isNeg() && !x.isZero() ? '-' + str : str;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal rounded to a maximum of `sd`
|
||||
* significant digits using rounding mode `rm`, or to `precision` and `rounding` respectively if
|
||||
* omitted.
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 1 to MAX_DIGITS inclusive.
|
||||
* [rm] {number} Rounding mode. Integer, 0 to 8 inclusive.
|
||||
*
|
||||
* 'toSD() digits out of range: {sd}'
|
||||
* 'toSD() digits not an integer: {sd}'
|
||||
* 'toSD() rounding mode not an integer: {rm}'
|
||||
* 'toSD() rounding mode out of range: {rm}'
|
||||
*
|
||||
*/
|
||||
P.toSignificantDigits = P.toSD = function (sd, rm) {
|
||||
var x = this,
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (sd === void 0) {
|
||||
sd = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
} else {
|
||||
checkInt32(sd, 1, MAX_DIGITS);
|
||||
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
}
|
||||
|
||||
return finalise(new Ctor(x), sd, rm);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal.
|
||||
*
|
||||
* Return exponential notation if this Decimal has a positive exponent equal to or greater than
|
||||
* `toExpPos`, or a negative exponent equal to or less than `toExpNeg`.
|
||||
*
|
||||
*/
|
||||
P.toString = function () {
|
||||
var x = this,
|
||||
Ctor = x.constructor,
|
||||
str = finiteToString(x, x.e <= Ctor.toExpNeg || x.e >= Ctor.toExpPos);
|
||||
|
||||
return x.isNeg() && !x.isZero() ? '-' + str : str;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of this Decimal truncated to a whole number.
|
||||
*
|
||||
*/
|
||||
P.truncated = P.trunc = function () {
|
||||
return finalise(new this.constructor(this), this.e + 1, 1);
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
* Return a string representing the value of this Decimal.
|
||||
* Unlike `toString`, negative zero will include the minus sign.
|
||||
*
|
||||
*/
|
||||
P.valueOf = P.toJSON = function () {
|
||||
var x = this,
|
||||
Ctor = x.constructor,
|
||||
str = finiteToString(x, x.e <= Ctor.toExpNeg || x.e >= Ctor.toExpPos);
|
||||
|
||||
return x.isNeg() ? '-' + str : str;
|
||||
};
|
||||
|
||||
|
||||
/*
|
||||
// Add aliases to match BigDecimal method names.
|
||||
// P.add = P.plus;
|
||||
P.subtract = P.minus;
|
||||
P.multiply = P.times;
|
||||
P.divide = P.div;
|
||||
P.remainder = P.mod;
|
||||
P.compareTo = P.cmp;
|
||||
P.negate = P.neg;
|
||||
*/
|
||||
|
||||
|
||||
// Helper functions for Decimal.prototype (P) and/or Decimal methods, and their callers.
|
||||
|
||||
|
||||
/*
|
||||
* digitsToString P.cubeRoot, P.logarithm, P.squareRoot, P.toFraction, P.toPower,
|
||||
* finiteToString, naturalExponential, naturalLogarithm
|
||||
* checkInt32 P.toDecimalPlaces, P.toExponential, P.toFixed, P.toNearest,
|
||||
* P.toPrecision, P.toSignificantDigits, toStringBinary, random
|
||||
* checkRoundingDigits P.logarithm, P.toPower, naturalExponential, naturalLogarithm
|
||||
* convertBase toStringBinary, parseOther
|
||||
* cos P.cos
|
||||
* divide P.atanh, P.cubeRoot, P.dividedBy, P.dividedToIntegerBy,
|
||||
* P.logarithm, P.modulo, P.squareRoot, P.tan, P.tanh, P.toFraction,
|
||||
* P.toNearest, toStringBinary, naturalExponential, naturalLogarithm,
|
||||
* taylorSeries, atan2, parseOther
|
||||
* finalise P.absoluteValue, P.atan, P.atanh, P.ceil, P.cos, P.cosh,
|
||||
* P.cubeRoot, P.dividedToIntegerBy, P.floor, P.logarithm, P.minus,
|
||||
* P.modulo, P.negated, P.plus, P.round, P.sin, P.sinh, P.squareRoot,
|
||||
* P.tan, P.times, P.toDecimalPlaces, P.toExponential, P.toFixed,
|
||||
* P.toNearest, P.toPower, P.toPrecision, P.toSignificantDigits,
|
||||
* P.truncated, divide, getLn10, getPi, naturalExponential,
|
||||
* naturalLogarithm, ceil, floor, round, trunc
|
||||
* finiteToString P.toExponential, P.toFixed, P.toPrecision, P.toString, P.valueOf,
|
||||
* toStringBinary
|
||||
* getBase10Exponent P.minus, P.plus, P.times, parseOther
|
||||
* getLn10 P.logarithm, naturalLogarithm
|
||||
* getPi P.acos, P.asin, P.atan, toLessThanHalfPi, atan2
|
||||
* getPrecision P.precision, P.toFraction
|
||||
* getZeroString digitsToString, finiteToString
|
||||
* intPow P.toPower, parseOther
|
||||
* isOdd toLessThanHalfPi
|
||||
* maxOrMin max, min
|
||||
* naturalExponential P.naturalExponential, P.toPower
|
||||
* naturalLogarithm P.acosh, P.asinh, P.atanh, P.logarithm, P.naturalLogarithm,
|
||||
* P.toPower, naturalExponential
|
||||
* nonFiniteToString finiteToString, toStringBinary
|
||||
* parseDecimal Decimal
|
||||
* parseOther Decimal
|
||||
* sin P.sin
|
||||
* taylorSeries P.cosh, P.sinh, cos, sin
|
||||
* toLessThanHalfPi P.cos, P.sin
|
||||
* toStringBinary P.toBinary, P.toHexadecimal, P.toOctal
|
||||
* truncate intPow
|
||||
*
|
||||
* Throws: P.logarithm, P.precision, P.toFraction, checkInt32, getLn10, getPi,
|
||||
* naturalLogarithm, config, parseOther, random, Decimal
|
||||
*/
|
||||
|
||||
|
||||
function digitsToString(d) {
|
||||
var i, k, ws,
|
||||
indexOfLastWord = d.length - 1,
|
||||
str = '',
|
||||
w = d[0];
|
||||
|
||||
if (indexOfLastWord > 0) {
|
||||
str += w;
|
||||
for (i = 1; i < indexOfLastWord; i++) {
|
||||
ws = d[i] + '';
|
||||
k = LOG_BASE - ws.length;
|
||||
if (k) str += getZeroString(k);
|
||||
str += ws;
|
||||
}
|
||||
|
||||
w = d[i];
|
||||
ws = w + '';
|
||||
k = LOG_BASE - ws.length;
|
||||
if (k) str += getZeroString(k);
|
||||
} else if (w === 0) {
|
||||
return '0';
|
||||
}
|
||||
|
||||
// Remove trailing zeros of last w.
|
||||
for (; w % 10 === 0;) w /= 10;
|
||||
|
||||
return str + w;
|
||||
}
|
||||
|
||||
|
||||
function checkInt32(i, min, max) {
|
||||
if (i !== ~~i || i < min || i > max) {
|
||||
throw Error(invalidArgument + i);
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Check 5 rounding digits if `repeating` is null, 4 otherwise.
|
||||
* `repeating == null` if caller is `log` or `pow`,
|
||||
* `repeating != null` if caller is `naturalLogarithm` or `naturalExponential`.
|
||||
*/
|
||||
function checkRoundingDigits(d, i, rm, repeating) {
|
||||
var di, k, r, rd;
|
||||
|
||||
// Get the length of the first word of the array d.
|
||||
for (k = d[0]; k >= 10; k /= 10) --i;
|
||||
|
||||
// Is the rounding digit in the first word of d?
|
||||
if (--i < 0) {
|
||||
i += LOG_BASE;
|
||||
di = 0;
|
||||
} else {
|
||||
di = Math.ceil((i + 1) / LOG_BASE);
|
||||
i %= LOG_BASE;
|
||||
}
|
||||
|
||||
// i is the index (0 - 6) of the rounding digit.
|
||||
// E.g. if within the word 3487563 the first rounding digit is 5,
|
||||
// then i = 4, k = 1000, rd = 3487563 % 1000 = 563
|
||||
k = mathpow(10, LOG_BASE - i);
|
||||
rd = d[di] % k | 0;
|
||||
|
||||
if (repeating == null) {
|
||||
if (i < 3) {
|
||||
if (i == 0) rd = rd / 100 | 0;
|
||||
else if (i == 1) rd = rd / 10 | 0;
|
||||
r = rm < 4 && rd == 99999 || rm > 3 && rd == 49999 || rd == 50000 || rd == 0;
|
||||
} else {
|
||||
r = (rm < 4 && rd + 1 == k || rm > 3 && rd + 1 == k / 2) &&
|
||||
(d[di + 1] / k / 100 | 0) == mathpow(10, i - 2) - 1 ||
|
||||
(rd == k / 2 || rd == 0) && (d[di + 1] / k / 100 | 0) == 0;
|
||||
}
|
||||
} else {
|
||||
if (i < 4) {
|
||||
if (i == 0) rd = rd / 1000 | 0;
|
||||
else if (i == 1) rd = rd / 100 | 0;
|
||||
else if (i == 2) rd = rd / 10 | 0;
|
||||
r = (repeating || rm < 4) && rd == 9999 || !repeating && rm > 3 && rd == 4999;
|
||||
} else {
|
||||
r = ((repeating || rm < 4) && rd + 1 == k ||
|
||||
(!repeating && rm > 3) && rd + 1 == k / 2) &&
|
||||
(d[di + 1] / k / 1000 | 0) == mathpow(10, i - 3) - 1;
|
||||
}
|
||||
}
|
||||
|
||||
return r;
|
||||
}
|
||||
|
||||
|
||||
// Convert string of `baseIn` to an array of numbers of `baseOut`.
|
||||
// Eg. convertBase('255', 10, 16) returns [15, 15].
|
||||
// Eg. convertBase('ff', 16, 10) returns [2, 5, 5].
|
||||
function convertBase(str, baseIn, baseOut) {
|
||||
var j,
|
||||
arr = [0],
|
||||
arrL,
|
||||
i = 0,
|
||||
strL = str.length;
|
||||
|
||||
for (; i < strL;) {
|
||||
for (arrL = arr.length; arrL--;) arr[arrL] *= baseIn;
|
||||
arr[0] += NUMERALS.indexOf(str.charAt(i++));
|
||||
for (j = 0; j < arr.length; j++) {
|
||||
if (arr[j] > baseOut - 1) {
|
||||
if (arr[j + 1] === void 0) arr[j + 1] = 0;
|
||||
arr[j + 1] += arr[j] / baseOut | 0;
|
||||
arr[j] %= baseOut;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return arr.reverse();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* cos(x) = 1 - x^2/2! + x^4/4! - ...
|
||||
* |x| < pi/2
|
||||
*
|
||||
*/
|
||||
function cosine(Ctor, x) {
|
||||
var k, y,
|
||||
len = x.d.length;
|
||||
|
||||
// Argument reduction: cos(4x) = 8*(cos^4(x) - cos^2(x)) + 1
|
||||
// i.e. cos(x) = 8*(cos^4(x/4) - cos^2(x/4)) + 1
|
||||
|
||||
// Estimate the optimum number of times to use the argument reduction.
|
||||
if (len < 32) {
|
||||
k = Math.ceil(len / 3);
|
||||
y = Math.pow(4, -k).toString();
|
||||
} else {
|
||||
k = 16;
|
||||
y = '2.3283064365386962890625e-10';
|
||||
}
|
||||
|
||||
Ctor.precision += k;
|
||||
|
||||
x = taylorSeries(Ctor, 1, x.times(y), new Ctor(1));
|
||||
|
||||
// Reverse argument reduction
|
||||
for (var i = k; i--;) {
|
||||
var cos2x = x.times(x);
|
||||
x = cos2x.times(cos2x).minus(cos2x).times(8).plus(1);
|
||||
}
|
||||
|
||||
Ctor.precision -= k;
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Perform division in the specified base.
|
||||
*/
|
||||
var divide = (function () {
|
||||
|
||||
// Assumes non-zero x and k, and hence non-zero result.
|
||||
function multiplyInteger(x, k, base) {
|
||||
var temp,
|
||||
carry = 0,
|
||||
i = x.length;
|
||||
|
||||
for (x = x.slice(); i--;) {
|
||||
temp = x[i] * k + carry;
|
||||
x[i] = temp % base | 0;
|
||||
carry = temp / base | 0;
|
||||
}
|
||||
|
||||
if (carry) x.unshift(carry);
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
function compare(a, b, aL, bL) {
|
||||
var i, r;
|
||||
|
||||
if (aL != bL) {
|
||||
r = aL > bL ? 1 : -1;
|
||||
} else {
|
||||
for (i = r = 0; i < aL; i++) {
|
||||
if (a[i] != b[i]) {
|
||||
r = a[i] > b[i] ? 1 : -1;
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return r;
|
||||
}
|
||||
|
||||
function subtract(a, b, aL, base) {
|
||||
var i = 0;
|
||||
|
||||
// Subtract b from a.
|
||||
for (; aL--;) {
|
||||
a[aL] -= i;
|
||||
i = a[aL] < b[aL] ? 1 : 0;
|
||||
a[aL] = i * base + a[aL] - b[aL];
|
||||
}
|
||||
|
||||
// Remove leading zeros.
|
||||
for (; !a[0] && a.length > 1;) a.shift();
|
||||
}
|
||||
|
||||
return function (x, y, pr, rm, dp, base) {
|
||||
var cmp, e, i, k, logBase, more, prod, prodL, q, qd, rem, remL, rem0, sd, t, xi, xL, yd0,
|
||||
yL, yz,
|
||||
Ctor = x.constructor,
|
||||
sign = x.s == y.s ? 1 : -1,
|
||||
xd = x.d,
|
||||
yd = y.d;
|
||||
|
||||
// Either NaN, Infinity or 0?
|
||||
if (!xd || !xd[0] || !yd || !yd[0]) {
|
||||
|
||||
return new Ctor(// Return NaN if either NaN, or both Infinity or 0.
|
||||
!x.s || !y.s || (xd ? yd && xd[0] == yd[0] : !yd) ? NaN :
|
||||
|
||||
// Return ±0 if x is 0 or y is ±Infinity, or return ±Infinity as y is 0.
|
||||
xd && xd[0] == 0 || !yd ? sign * 0 : sign / 0);
|
||||
}
|
||||
|
||||
if (base) {
|
||||
logBase = 1;
|
||||
e = x.e - y.e;
|
||||
} else {
|
||||
base = BASE;
|
||||
logBase = LOG_BASE;
|
||||
e = mathfloor(x.e / logBase) - mathfloor(y.e / logBase);
|
||||
}
|
||||
|
||||
yL = yd.length;
|
||||
xL = xd.length;
|
||||
q = new Ctor(sign);
|
||||
qd = q.d = [];
|
||||
|
||||
// Result exponent may be one less than e.
|
||||
// The digit array of a Decimal from toStringBinary may have trailing zeros.
|
||||
for (i = 0; yd[i] == (xd[i] || 0); i++);
|
||||
|
||||
if (yd[i] > (xd[i] || 0)) e--;
|
||||
|
||||
if (pr == null) {
|
||||
sd = pr = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
} else if (dp) {
|
||||
sd = pr + (x.e - y.e) + 1;
|
||||
} else {
|
||||
sd = pr;
|
||||
}
|
||||
|
||||
if (sd < 0) {
|
||||
qd.push(1);
|
||||
more = true;
|
||||
} else {
|
||||
|
||||
// Convert precision in number of base 10 digits to base 1e7 digits.
|
||||
sd = sd / logBase + 2 | 0;
|
||||
i = 0;
|
||||
|
||||
// divisor < 1e7
|
||||
if (yL == 1) {
|
||||
k = 0;
|
||||
yd = yd[0];
|
||||
sd++;
|
||||
|
||||
// k is the carry.
|
||||
for (; (i < xL || k) && sd--; i++) {
|
||||
t = k * base + (xd[i] || 0);
|
||||
qd[i] = t / yd | 0;
|
||||
k = t % yd | 0;
|
||||
}
|
||||
|
||||
more = k || i < xL;
|
||||
|
||||
// divisor >= 1e7
|
||||
} else {
|
||||
|
||||
// Normalise xd and yd so highest order digit of yd is >= base/2
|
||||
k = base / (yd[0] + 1) | 0;
|
||||
|
||||
if (k > 1) {
|
||||
yd = multiplyInteger(yd, k, base);
|
||||
xd = multiplyInteger(xd, k, base);
|
||||
yL = yd.length;
|
||||
xL = xd.length;
|
||||
}
|
||||
|
||||
xi = yL;
|
||||
rem = xd.slice(0, yL);
|
||||
remL = rem.length;
|
||||
|
||||
// Add zeros to make remainder as long as divisor.
|
||||
for (; remL < yL;) rem[remL++] = 0;
|
||||
|
||||
yz = yd.slice();
|
||||
yz.unshift(0);
|
||||
yd0 = yd[0];
|
||||
|
||||
if (yd[1] >= base / 2) ++yd0;
|
||||
|
||||
do {
|
||||
k = 0;
|
||||
|
||||
// Compare divisor and remainder.
|
||||
cmp = compare(yd, rem, yL, remL);
|
||||
|
||||
// If divisor < remainder.
|
||||
if (cmp < 0) {
|
||||
|
||||
// Calculate trial digit, k.
|
||||
rem0 = rem[0];
|
||||
if (yL != remL) rem0 = rem0 * base + (rem[1] || 0);
|
||||
|
||||
// k will be how many times the divisor goes into the current remainder.
|
||||
k = rem0 / yd0 | 0;
|
||||
|
||||
// Algorithm:
|
||||
// 1. product = divisor * trial digit (k)
|
||||
// 2. if product > remainder: product -= divisor, k--
|
||||
// 3. remainder -= product
|
||||
// 4. if product was < remainder at 2:
|
||||
// 5. compare new remainder and divisor
|
||||
// 6. If remainder > divisor: remainder -= divisor, k++
|
||||
|
||||
if (k > 1) {
|
||||
if (k >= base) k = base - 1;
|
||||
|
||||
// product = divisor * trial digit.
|
||||
prod = multiplyInteger(yd, k, base);
|
||||
prodL = prod.length;
|
||||
remL = rem.length;
|
||||
|
||||
// Compare product and remainder.
|
||||
cmp = compare(prod, rem, prodL, remL);
|
||||
|
||||
// product > remainder.
|
||||
if (cmp == 1) {
|
||||
k--;
|
||||
|
||||
// Subtract divisor from product.
|
||||
subtract(prod, yL < prodL ? yz : yd, prodL, base);
|
||||
}
|
||||
} else {
|
||||
|
||||
// cmp is -1.
|
||||
// If k is 0, there is no need to compare yd and rem again below, so change cmp to 1
|
||||
// to avoid it. If k is 1 there is a need to compare yd and rem again below.
|
||||
if (k == 0) cmp = k = 1;
|
||||
prod = yd.slice();
|
||||
}
|
||||
|
||||
prodL = prod.length;
|
||||
if (prodL < remL) prod.unshift(0);
|
||||
|
||||
// Subtract product from remainder.
|
||||
subtract(rem, prod, remL, base);
|
||||
|
||||
// If product was < previous remainder.
|
||||
if (cmp == -1) {
|
||||
remL = rem.length;
|
||||
|
||||
// Compare divisor and new remainder.
|
||||
cmp = compare(yd, rem, yL, remL);
|
||||
|
||||
// If divisor < new remainder, subtract divisor from remainder.
|
||||
if (cmp < 1) {
|
||||
k++;
|
||||
|
||||
// Subtract divisor from remainder.
|
||||
subtract(rem, yL < remL ? yz : yd, remL, base);
|
||||
}
|
||||
}
|
||||
|
||||
remL = rem.length;
|
||||
} else if (cmp === 0) {
|
||||
k++;
|
||||
rem = [0];
|
||||
} // if cmp === 1, k will be 0
|
||||
|
||||
// Add the next digit, k, to the result array.
|
||||
qd[i++] = k;
|
||||
|
||||
// Update the remainder.
|
||||
if (cmp && rem[0]) {
|
||||
rem[remL++] = xd[xi] || 0;
|
||||
} else {
|
||||
rem = [xd[xi]];
|
||||
remL = 1;
|
||||
}
|
||||
|
||||
} while ((xi++ < xL || rem[0] !== void 0) && sd--);
|
||||
|
||||
more = rem[0] !== void 0;
|
||||
}
|
||||
|
||||
// Leading zero?
|
||||
if (!qd[0]) qd.shift();
|
||||
}
|
||||
|
||||
// logBase is 1 when divide is being used for base conversion.
|
||||
if (logBase == 1) {
|
||||
q.e = e;
|
||||
inexact = more;
|
||||
} else {
|
||||
|
||||
// To calculate q.e, first get the number of digits of qd[0].
|
||||
for (i = 1, k = qd[0]; k >= 10; k /= 10) i++;
|
||||
q.e = i + e * logBase - 1;
|
||||
|
||||
finalise(q, dp ? pr + q.e + 1 : pr, rm, more);
|
||||
}
|
||||
|
||||
return q;
|
||||
};
|
||||
})();
|
||||
|
||||
|
||||
/*
|
||||
* Round `x` to `sd` significant digits using rounding mode `rm`.
|
||||
* Check for over/under-flow.
|
||||
*/
|
||||
function finalise(x, sd, rm, isTruncated) {
|
||||
var digits, i, j, k, rd, roundUp, w, xd, xdi,
|
||||
Ctor = x.constructor;
|
||||
|
||||
// Don't round if sd is null or undefined.
|
||||
out: if (sd != null) {
|
||||
xd = x.d;
|
||||
|
||||
// Infinity/NaN.
|
||||
if (!xd) return x;
|
||||
|
||||
// rd: the rounding digit, i.e. the digit after the digit that may be rounded up.
|
||||
// w: the word of xd containing rd, a base 1e7 number.
|
||||
// xdi: the index of w within xd.
|
||||
// digits: the number of digits of w.
|
||||
// i: what would be the index of rd within w if all the numbers were 7 digits long (i.e. if
|
||||
// they had leading zeros)
|
||||
// j: if > 0, the actual index of rd within w (if < 0, rd is a leading zero).
|
||||
|
||||
// Get the length of the first word of the digits array xd.
|
||||
for (digits = 1, k = xd[0]; k >= 10; k /= 10) digits++;
|
||||
i = sd - digits;
|
||||
|
||||
// Is the rounding digit in the first word of xd?
|
||||
if (i < 0) {
|
||||
i += LOG_BASE;
|
||||
j = sd;
|
||||
w = xd[xdi = 0];
|
||||
|
||||
// Get the rounding digit at index j of w.
|
||||
rd = w / mathpow(10, digits - j - 1) % 10 | 0;
|
||||
} else {
|
||||
xdi = Math.ceil((i + 1) / LOG_BASE);
|
||||
k = xd.length;
|
||||
if (xdi >= k) {
|
||||
if (isTruncated) {
|
||||
|
||||
// Needed by `naturalExponential`, `naturalLogarithm` and `squareRoot`.
|
||||
for (; k++ <= xdi;) xd.push(0);
|
||||
w = rd = 0;
|
||||
digits = 1;
|
||||
i %= LOG_BASE;
|
||||
j = i - LOG_BASE + 1;
|
||||
} else {
|
||||
break out;
|
||||
}
|
||||
} else {
|
||||
w = k = xd[xdi];
|
||||
|
||||
// Get the number of digits of w.
|
||||
for (digits = 1; k >= 10; k /= 10) digits++;
|
||||
|
||||
// Get the index of rd within w.
|
||||
i %= LOG_BASE;
|
||||
|
||||
// Get the index of rd within w, adjusted for leading zeros.
|
||||
// The number of leading zeros of w is given by LOG_BASE - digits.
|
||||
j = i - LOG_BASE + digits;
|
||||
|
||||
// Get the rounding digit at index j of w.
|
||||
rd = j < 0 ? 0 : w / mathpow(10, digits - j - 1) % 10 | 0;
|
||||
}
|
||||
}
|
||||
|
||||
// Are there any non-zero digits after the rounding digit?
|
||||
isTruncated = isTruncated || sd < 0 ||
|
||||
xd[xdi + 1] !== void 0 || (j < 0 ? w : w % mathpow(10, digits - j - 1));
|
||||
|
||||
// The expression `w % mathpow(10, digits - j - 1)` returns all the digits of w to the right
|
||||
// of the digit at (left-to-right) index j, e.g. if w is 908714 and j is 2, the expression
|
||||
// will give 714.
|
||||
|
||||
roundUp = rm < 4
|
||||
? (rd || isTruncated) && (rm == 0 || rm == (x.s < 0 ? 3 : 2))
|
||||
: rd > 5 || rd == 5 && (rm == 4 || isTruncated || rm == 6 &&
|
||||
|
||||
// Check whether the digit to the left of the rounding digit is odd.
|
||||
((i > 0 ? j > 0 ? w / mathpow(10, digits - j) : 0 : xd[xdi - 1]) % 10) & 1 ||
|
||||
rm == (x.s < 0 ? 8 : 7));
|
||||
|
||||
if (sd < 1 || !xd[0]) {
|
||||
xd.length = 0;
|
||||
if (roundUp) {
|
||||
|
||||
// Convert sd to decimal places.
|
||||
sd -= x.e + 1;
|
||||
|
||||
// 1, 0.1, 0.01, 0.001, 0.0001 etc.
|
||||
xd[0] = mathpow(10, (LOG_BASE - sd % LOG_BASE) % LOG_BASE);
|
||||
x.e = -sd || 0;
|
||||
} else {
|
||||
|
||||
// Zero.
|
||||
xd[0] = x.e = 0;
|
||||
}
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
// Remove excess digits.
|
||||
if (i == 0) {
|
||||
xd.length = xdi;
|
||||
k = 1;
|
||||
xdi--;
|
||||
} else {
|
||||
xd.length = xdi + 1;
|
||||
k = mathpow(10, LOG_BASE - i);
|
||||
|
||||
// E.g. 56700 becomes 56000 if 7 is the rounding digit.
|
||||
// j > 0 means i > number of leading zeros of w.
|
||||
xd[xdi] = j > 0 ? (w / mathpow(10, digits - j) % mathpow(10, j) | 0) * k : 0;
|
||||
}
|
||||
|
||||
if (roundUp) {
|
||||
for (;;) {
|
||||
|
||||
// Is the digit to be rounded up in the first word of xd?
|
||||
if (xdi == 0) {
|
||||
|
||||
// i will be the length of xd[0] before k is added.
|
||||
for (i = 1, j = xd[0]; j >= 10; j /= 10) i++;
|
||||
j = xd[0] += k;
|
||||
for (k = 1; j >= 10; j /= 10) k++;
|
||||
|
||||
// if i != k the length has increased.
|
||||
if (i != k) {
|
||||
x.e++;
|
||||
if (xd[0] == BASE) xd[0] = 1;
|
||||
}
|
||||
|
||||
break;
|
||||
} else {
|
||||
xd[xdi] += k;
|
||||
if (xd[xdi] != BASE) break;
|
||||
xd[xdi--] = 0;
|
||||
k = 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// Remove trailing zeros.
|
||||
for (i = xd.length; xd[--i] === 0;) xd.pop();
|
||||
}
|
||||
|
||||
if (external) {
|
||||
|
||||
// Overflow?
|
||||
if (x.e > Ctor.maxE) {
|
||||
|
||||
// Infinity.
|
||||
x.d = null;
|
||||
x.e = NaN;
|
||||
|
||||
// Underflow?
|
||||
} else if (x.e < Ctor.minE) {
|
||||
|
||||
// Zero.
|
||||
x.e = 0;
|
||||
x.d = [0];
|
||||
// Ctor.underflow = true;
|
||||
} // else Ctor.underflow = false;
|
||||
}
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
function finiteToString(x, isExp, sd) {
|
||||
if (!x.isFinite()) return nonFiniteToString(x);
|
||||
var k,
|
||||
e = x.e,
|
||||
str = digitsToString(x.d),
|
||||
len = str.length;
|
||||
|
||||
if (isExp) {
|
||||
if (sd && (k = sd - len) > 0) {
|
||||
str = str.charAt(0) + '.' + str.slice(1) + getZeroString(k);
|
||||
} else if (len > 1) {
|
||||
str = str.charAt(0) + '.' + str.slice(1);
|
||||
}
|
||||
|
||||
str = str + (x.e < 0 ? 'e' : 'e+') + x.e;
|
||||
} else if (e < 0) {
|
||||
str = '0.' + getZeroString(-e - 1) + str;
|
||||
if (sd && (k = sd - len) > 0) str += getZeroString(k);
|
||||
} else if (e >= len) {
|
||||
str += getZeroString(e + 1 - len);
|
||||
if (sd && (k = sd - e - 1) > 0) str = str + '.' + getZeroString(k);
|
||||
} else {
|
||||
if ((k = e + 1) < len) str = str.slice(0, k) + '.' + str.slice(k);
|
||||
if (sd && (k = sd - len) > 0) {
|
||||
if (e + 1 === len) str += '.';
|
||||
str += getZeroString(k);
|
||||
}
|
||||
}
|
||||
|
||||
return str;
|
||||
}
|
||||
|
||||
|
||||
// Calculate the base 10 exponent from the base 1e7 exponent.
|
||||
function getBase10Exponent(digits, e) {
|
||||
var w = digits[0];
|
||||
|
||||
// Add the number of digits of the first word of the digits array.
|
||||
for ( e *= LOG_BASE; w >= 10; w /= 10) e++;
|
||||
return e;
|
||||
}
|
||||
|
||||
|
||||
function getLn10(Ctor, sd, pr) {
|
||||
if (sd > LN10_PRECISION) {
|
||||
|
||||
// Reset global state in case the exception is caught.
|
||||
external = true;
|
||||
if (pr) Ctor.precision = pr;
|
||||
throw Error(precisionLimitExceeded);
|
||||
}
|
||||
return finalise(new Ctor(LN10), sd, 1, true);
|
||||
}
|
||||
|
||||
|
||||
function getPi(Ctor, sd, rm) {
|
||||
if (sd > PI_PRECISION) throw Error(precisionLimitExceeded);
|
||||
return finalise(new Ctor(PI), sd, rm, true);
|
||||
}
|
||||
|
||||
|
||||
function getPrecision(digits) {
|
||||
var w = digits.length - 1,
|
||||
len = w * LOG_BASE + 1;
|
||||
|
||||
w = digits[w];
|
||||
|
||||
// If non-zero...
|
||||
if (w) {
|
||||
|
||||
// Subtract the number of trailing zeros of the last word.
|
||||
for (; w % 10 == 0; w /= 10) len--;
|
||||
|
||||
// Add the number of digits of the first word.
|
||||
for (w = digits[0]; w >= 10; w /= 10) len++;
|
||||
}
|
||||
|
||||
return len;
|
||||
}
|
||||
|
||||
|
||||
function getZeroString(k) {
|
||||
var zs = '';
|
||||
for (; k--;) zs += '0';
|
||||
return zs;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the value of Decimal `x` to the power `n`, where `n` is an
|
||||
* integer of type number.
|
||||
*
|
||||
* Implements 'exponentiation by squaring'. Called by `pow` and `parseOther`.
|
||||
*
|
||||
*/
|
||||
function intPow(Ctor, x, n, pr) {
|
||||
var isTruncated,
|
||||
r = new Ctor(1),
|
||||
|
||||
// Max n of 9007199254740991 takes 53 loop iterations.
|
||||
// Maximum digits array length; leaves [28, 34] guard digits.
|
||||
k = Math.ceil(pr / LOG_BASE + 4);
|
||||
|
||||
external = false;
|
||||
|
||||
for (;;) {
|
||||
if (n % 2) {
|
||||
r = r.times(x);
|
||||
if (truncate(r.d, k)) isTruncated = true;
|
||||
}
|
||||
|
||||
n = mathfloor(n / 2);
|
||||
if (n === 0) {
|
||||
|
||||
// To ensure correct rounding when r.d is truncated, increment the last word if it is zero.
|
||||
n = r.d.length - 1;
|
||||
if (isTruncated && r.d[n] === 0) ++r.d[n];
|
||||
break;
|
||||
}
|
||||
|
||||
x = x.times(x);
|
||||
truncate(x.d, k);
|
||||
}
|
||||
|
||||
external = true;
|
||||
|
||||
return r;
|
||||
}
|
||||
|
||||
|
||||
function isOdd(n) {
|
||||
return n.d[n.d.length - 1] & 1;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Handle `max` and `min`. `ltgt` is 'lt' or 'gt'.
|
||||
*/
|
||||
function maxOrMin(Ctor, args, ltgt) {
|
||||
var y,
|
||||
x = new Ctor(args[0]),
|
||||
i = 0;
|
||||
|
||||
for (; ++i < args.length;) {
|
||||
y = new Ctor(args[i]);
|
||||
if (!y.s) {
|
||||
x = y;
|
||||
break;
|
||||
} else if (x[ltgt](y)) {
|
||||
x = y;
|
||||
}
|
||||
}
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural exponential of `x` rounded to `sd` significant
|
||||
* digits.
|
||||
*
|
||||
* Taylor/Maclaurin series.
|
||||
*
|
||||
* exp(x) = x^0/0! + x^1/1! + x^2/2! + x^3/3! + ...
|
||||
*
|
||||
* Argument reduction:
|
||||
* Repeat x = x / 32, k += 5, until |x| < 0.1
|
||||
* exp(x) = exp(x / 2^k)^(2^k)
|
||||
*
|
||||
* Previously, the argument was initially reduced by
|
||||
* exp(x) = exp(r) * 10^k where r = x - k * ln10, k = floor(x / ln10)
|
||||
* to first put r in the range [0, ln10], before dividing by 32 until |x| < 0.1, but this was
|
||||
* found to be slower than just dividing repeatedly by 32 as above.
|
||||
*
|
||||
* Max integer argument: exp('20723265836946413') = 6.3e+9000000000000000
|
||||
* Min integer argument: exp('-20723265836946411') = 1.2e-9000000000000000
|
||||
* (Math object integer min/max: Math.exp(709) = 8.2e+307, Math.exp(-745) = 5e-324)
|
||||
*
|
||||
* exp(Infinity) = Infinity
|
||||
* exp(-Infinity) = 0
|
||||
* exp(NaN) = NaN
|
||||
* exp(±0) = 1
|
||||
*
|
||||
* exp(x) is non-terminating for any finite, non-zero x.
|
||||
*
|
||||
* The result will always be correctly rounded.
|
||||
*
|
||||
*/
|
||||
function naturalExponential(x, sd) {
|
||||
var denominator, guard, j, pow, sum, t, wpr,
|
||||
rep = 0,
|
||||
i = 0,
|
||||
k = 0,
|
||||
Ctor = x.constructor,
|
||||
rm = Ctor.rounding,
|
||||
pr = Ctor.precision;
|
||||
|
||||
// 0/NaN/Infinity?
|
||||
if (!x.d || !x.d[0] || x.e > 17) {
|
||||
|
||||
return new Ctor(x.d
|
||||
? !x.d[0] ? 1 : x.s < 0 ? 0 : 1 / 0
|
||||
: x.s ? x.s < 0 ? 0 : x : 0 / 0);
|
||||
}
|
||||
|
||||
if (sd == null) {
|
||||
external = false;
|
||||
wpr = pr;
|
||||
} else {
|
||||
wpr = sd;
|
||||
}
|
||||
|
||||
t = new Ctor(0.03125);
|
||||
|
||||
// while abs(x) >= 0.1
|
||||
while (x.e > -2) {
|
||||
|
||||
// x = x / 2^5
|
||||
x = x.times(t);
|
||||
k += 5;
|
||||
}
|
||||
|
||||
// Use 2 * log10(2^k) + 5 (empirically derived) to estimate the increase in precision
|
||||
// necessary to ensure the first 4 rounding digits are correct.
|
||||
guard = Math.log(mathpow(2, k)) / Math.LN10 * 2 + 5 | 0;
|
||||
wpr += guard;
|
||||
denominator = pow = sum = new Ctor(1);
|
||||
Ctor.precision = wpr;
|
||||
|
||||
for (;;) {
|
||||
pow = finalise(pow.times(x), wpr, 1);
|
||||
denominator = denominator.times(++i);
|
||||
t = sum.plus(divide(pow, denominator, wpr, 1));
|
||||
|
||||
if (digitsToString(t.d).slice(0, wpr) === digitsToString(sum.d).slice(0, wpr)) {
|
||||
j = k;
|
||||
while (j--) sum = finalise(sum.times(sum), wpr, 1);
|
||||
|
||||
// Check to see if the first 4 rounding digits are [49]999.
|
||||
// If so, repeat the summation with a higher precision, otherwise
|
||||
// e.g. with precision: 18, rounding: 1
|
||||
// exp(18.404272462595034083567793919843761) = 98372560.1229999999 (should be 98372560.123)
|
||||
// `wpr - guard` is the index of first rounding digit.
|
||||
if (sd == null) {
|
||||
|
||||
if (rep < 3 && checkRoundingDigits(sum.d, wpr - guard, rm, rep)) {
|
||||
Ctor.precision = wpr += 10;
|
||||
denominator = pow = t = new Ctor(1);
|
||||
i = 0;
|
||||
rep++;
|
||||
} else {
|
||||
return finalise(sum, Ctor.precision = pr, rm, external = true);
|
||||
}
|
||||
} else {
|
||||
Ctor.precision = pr;
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
|
||||
sum = t;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural logarithm of `x` rounded to `sd` significant
|
||||
* digits.
|
||||
*
|
||||
* ln(-n) = NaN
|
||||
* ln(0) = -Infinity
|
||||
* ln(-0) = -Infinity
|
||||
* ln(1) = 0
|
||||
* ln(Infinity) = Infinity
|
||||
* ln(-Infinity) = NaN
|
||||
* ln(NaN) = NaN
|
||||
*
|
||||
* ln(n) (n != 1) is non-terminating.
|
||||
*
|
||||
*/
|
||||
function naturalLogarithm(y, sd) {
|
||||
var c, c0, denominator, e, numerator, rep, sum, t, wpr, x1, x2,
|
||||
n = 1,
|
||||
guard = 10,
|
||||
x = y,
|
||||
xd = x.d,
|
||||
Ctor = x.constructor,
|
||||
rm = Ctor.rounding,
|
||||
pr = Ctor.precision;
|
||||
|
||||
// Is x negative or Infinity, NaN, 0 or 1?
|
||||
if (x.s < 0 || !xd || !xd[0] || !x.e && xd[0] == 1 && xd.length == 1) {
|
||||
return new Ctor(xd && !xd[0] ? -1 / 0 : x.s != 1 ? NaN : xd ? 0 : x);
|
||||
}
|
||||
|
||||
if (sd == null) {
|
||||
external = false;
|
||||
wpr = pr;
|
||||
} else {
|
||||
wpr = sd;
|
||||
}
|
||||
|
||||
Ctor.precision = wpr += guard;
|
||||
c = digitsToString(xd);
|
||||
c0 = c.charAt(0);
|
||||
|
||||
if (Math.abs(e = x.e) < 1.5e15) {
|
||||
|
||||
// Argument reduction.
|
||||
// The series converges faster the closer the argument is to 1, so using
|
||||
// ln(a^b) = b * ln(a), ln(a) = ln(a^b) / b
|
||||
// multiply the argument by itself until the leading digits of the significand are 7, 8, 9,
|
||||
// 10, 11, 12 or 13, recording the number of multiplications so the sum of the series can
|
||||
// later be divided by this number, then separate out the power of 10 using
|
||||
// ln(a*10^b) = ln(a) + b*ln(10).
|
||||
|
||||
// max n is 21 (gives 0.9, 1.0 or 1.1) (9e15 / 21 = 4.2e14).
|
||||
//while (c0 < 9 && c0 != 1 || c0 == 1 && c.charAt(1) > 1) {
|
||||
// max n is 6 (gives 0.7 - 1.3)
|
||||
while (c0 < 7 && c0 != 1 || c0 == 1 && c.charAt(1) > 3) {
|
||||
x = x.times(y);
|
||||
c = digitsToString(x.d);
|
||||
c0 = c.charAt(0);
|
||||
n++;
|
||||
}
|
||||
|
||||
e = x.e;
|
||||
|
||||
if (c0 > 1) {
|
||||
x = new Ctor('0.' + c);
|
||||
e++;
|
||||
} else {
|
||||
x = new Ctor(c0 + '.' + c.slice(1));
|
||||
}
|
||||
} else {
|
||||
|
||||
// The argument reduction method above may result in overflow if the argument y is a massive
|
||||
// number with exponent >= 1500000000000000 (9e15 / 6 = 1.5e15), so instead recall this
|
||||
// function using ln(x*10^e) = ln(x) + e*ln(10).
|
||||
t = getLn10(Ctor, wpr + 2, pr).times(e + '');
|
||||
x = naturalLogarithm(new Ctor(c0 + '.' + c.slice(1)), wpr - guard).plus(t);
|
||||
Ctor.precision = pr;
|
||||
|
||||
return sd == null ? finalise(x, pr, rm, external = true) : x;
|
||||
}
|
||||
|
||||
// x1 is x reduced to a value near 1.
|
||||
x1 = x;
|
||||
|
||||
// Taylor series.
|
||||
// ln(y) = ln((1 + x)/(1 - x)) = 2(x + x^3/3 + x^5/5 + x^7/7 + ...)
|
||||
// where x = (y - 1)/(y + 1) (|x| < 1)
|
||||
sum = numerator = x = divide(x.minus(1), x.plus(1), wpr, 1);
|
||||
x2 = finalise(x.times(x), wpr, 1);
|
||||
denominator = 3;
|
||||
|
||||
for (;;) {
|
||||
numerator = finalise(numerator.times(x2), wpr, 1);
|
||||
t = sum.plus(divide(numerator, new Ctor(denominator), wpr, 1));
|
||||
|
||||
if (digitsToString(t.d).slice(0, wpr) === digitsToString(sum.d).slice(0, wpr)) {
|
||||
sum = sum.times(2);
|
||||
|
||||
// Reverse the argument reduction. Check that e is not 0 because, besides preventing an
|
||||
// unnecessary calculation, -0 + 0 = +0 and to ensure correct rounding -0 needs to stay -0.
|
||||
if (e !== 0) sum = sum.plus(getLn10(Ctor, wpr + 2, pr).times(e + ''));
|
||||
sum = divide(sum, new Ctor(n), wpr, 1);
|
||||
|
||||
// Is rm > 3 and the first 4 rounding digits 4999, or rm < 4 (or the summation has
|
||||
// been repeated previously) and the first 4 rounding digits 9999?
|
||||
// If so, restart the summation with a higher precision, otherwise
|
||||
// e.g. with precision: 12, rounding: 1
|
||||
// ln(135520028.6126091714265381533) = 18.7246299999 when it should be 18.72463.
|
||||
// `wpr - guard` is the index of first rounding digit.
|
||||
if (sd == null) {
|
||||
if (checkRoundingDigits(sum.d, wpr - guard, rm, rep)) {
|
||||
Ctor.precision = wpr += guard;
|
||||
t = numerator = x = divide(x1.minus(1), x1.plus(1), wpr, 1);
|
||||
x2 = finalise(x.times(x), wpr, 1);
|
||||
denominator = rep = 1;
|
||||
} else {
|
||||
return finalise(sum, Ctor.precision = pr, rm, external = true);
|
||||
}
|
||||
} else {
|
||||
Ctor.precision = pr;
|
||||
return sum;
|
||||
}
|
||||
}
|
||||
|
||||
sum = t;
|
||||
denominator += 2;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
// ±Infinity, NaN.
|
||||
function nonFiniteToString(x) {
|
||||
// Unsigned.
|
||||
return String(x.s * x.s / 0);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Parse the value of a new Decimal `x` from string `str`.
|
||||
*/
|
||||
function parseDecimal(x, str) {
|
||||
var e, i, len;
|
||||
|
||||
// Decimal point?
|
||||
if ((e = str.indexOf('.')) > -1) str = str.replace('.', '');
|
||||
|
||||
// Exponential form?
|
||||
if ((i = str.search(/e/i)) > 0) {
|
||||
|
||||
// Determine exponent.
|
||||
if (e < 0) e = i;
|
||||
e += +str.slice(i + 1);
|
||||
str = str.substring(0, i);
|
||||
} else if (e < 0) {
|
||||
|
||||
// Integer.
|
||||
e = str.length;
|
||||
}
|
||||
|
||||
// Determine leading zeros.
|
||||
for (i = 0; str.charCodeAt(i) === 48; i++);
|
||||
|
||||
// Determine trailing zeros.
|
||||
for (len = str.length; str.charCodeAt(len - 1) === 48; --len);
|
||||
str = str.slice(i, len);
|
||||
|
||||
if (str) {
|
||||
len -= i;
|
||||
x.e = e = e - i - 1;
|
||||
x.d = [];
|
||||
|
||||
// Transform base
|
||||
|
||||
// e is the base 10 exponent.
|
||||
// i is where to slice str to get the first word of the digits array.
|
||||
i = (e + 1) % LOG_BASE;
|
||||
if (e < 0) i += LOG_BASE;
|
||||
|
||||
if (i < len) {
|
||||
if (i) x.d.push(+str.slice(0, i));
|
||||
for (len -= LOG_BASE; i < len;) x.d.push(+str.slice(i, i += LOG_BASE));
|
||||
str = str.slice(i);
|
||||
i = LOG_BASE - str.length;
|
||||
} else {
|
||||
i -= len;
|
||||
}
|
||||
|
||||
for (; i--;) str += '0';
|
||||
x.d.push(+str);
|
||||
|
||||
if (external) {
|
||||
|
||||
// Overflow?
|
||||
if (x.e > x.constructor.maxE) {
|
||||
|
||||
// Infinity.
|
||||
x.d = null;
|
||||
x.e = NaN;
|
||||
|
||||
// Underflow?
|
||||
} else if (x.e < x.constructor.minE) {
|
||||
|
||||
// Zero.
|
||||
x.e = 0;
|
||||
x.d = [0];
|
||||
// x.constructor.underflow = true;
|
||||
} // else x.constructor.underflow = false;
|
||||
}
|
||||
} else {
|
||||
|
||||
// Zero.
|
||||
x.e = 0;
|
||||
x.d = [0];
|
||||
}
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Parse the value of a new Decimal `x` from a string `str`, which is not a decimal value.
|
||||
*/
|
||||
function parseOther(x, str) {
|
||||
var base, Ctor, divisor, i, isFloat, len, p, xd, xe;
|
||||
|
||||
if (str === 'Infinity' || str === 'NaN') {
|
||||
if (!+str) x.s = NaN;
|
||||
x.e = NaN;
|
||||
x.d = null;
|
||||
return x;
|
||||
}
|
||||
|
||||
if (isHex.test(str)) {
|
||||
base = 16;
|
||||
str = str.toLowerCase();
|
||||
} else if (isBinary.test(str)) {
|
||||
base = 2;
|
||||
} else if (isOctal.test(str)) {
|
||||
base = 8;
|
||||
} else {
|
||||
throw Error(invalidArgument + str);
|
||||
}
|
||||
|
||||
// Is there a binary exponent part?
|
||||
i = str.search(/p/i);
|
||||
|
||||
if (i > 0) {
|
||||
p = +str.slice(i + 1);
|
||||
str = str.substring(2, i);
|
||||
} else {
|
||||
str = str.slice(2);
|
||||
}
|
||||
|
||||
// Convert `str` as an integer then divide the result by `base` raised to a power such that the
|
||||
// fraction part will be restored.
|
||||
i = str.indexOf('.');
|
||||
isFloat = i >= 0;
|
||||
Ctor = x.constructor;
|
||||
|
||||
if (isFloat) {
|
||||
str = str.replace('.', '');
|
||||
len = str.length;
|
||||
i = len - i;
|
||||
|
||||
// log[10](16) = 1.2041... , log[10](88) = 1.9444....
|
||||
divisor = intPow(Ctor, new Ctor(base), i, i * 2);
|
||||
}
|
||||
|
||||
xd = convertBase(str, base, BASE);
|
||||
xe = xd.length - 1;
|
||||
|
||||
// Remove trailing zeros.
|
||||
for (i = xe; xd[i] === 0; --i) xd.pop();
|
||||
if (i < 0) return new Ctor(x.s * 0);
|
||||
x.e = getBase10Exponent(xd, xe);
|
||||
x.d = xd;
|
||||
external = false;
|
||||
|
||||
// At what precision to perform the division to ensure exact conversion?
|
||||
// maxDecimalIntegerPartDigitCount = ceil(log[10](b) * otherBaseIntegerPartDigitCount)
|
||||
// log[10](2) = 0.30103, log[10](8) = 0.90309, log[10](16) = 1.20412
|
||||
// E.g. ceil(1.2 * 3) = 4, so up to 4 decimal digits are needed to represent 3 hex int digits.
|
||||
// maxDecimalFractionPartDigitCount = {Hex:4|Oct:3|Bin:1} * otherBaseFractionPartDigitCount
|
||||
// Therefore using 4 * the number of digits of str will always be enough.
|
||||
if (isFloat) x = divide(x, divisor, len * 4);
|
||||
|
||||
// Multiply by the binary exponent part if present.
|
||||
if (p) x = x.times(Math.abs(p) < 54 ? Math.pow(2, p) : Decimal.pow(2, p));
|
||||
external = true;
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* sin(x) = x - x^3/3! + x^5/5! - ...
|
||||
* |x| < pi/2
|
||||
*
|
||||
*/
|
||||
function sine(Ctor, x) {
|
||||
var k,
|
||||
len = x.d.length;
|
||||
|
||||
if (len < 3) return taylorSeries(Ctor, 2, x, x);
|
||||
|
||||
// Argument reduction: sin(5x) = 16*sin^5(x) - 20*sin^3(x) + 5*sin(x)
|
||||
// i.e. sin(x) = 16*sin^5(x/5) - 20*sin^3(x/5) + 5*sin(x/5)
|
||||
// and sin(x) = sin(x/5)(5 + sin^2(x/5)(16sin^2(x/5) - 20))
|
||||
|
||||
// Estimate the optimum number of times to use the argument reduction.
|
||||
k = 1.4 * Math.sqrt(len);
|
||||
k = k > 16 ? 16 : k | 0;
|
||||
|
||||
// Max k before Math.pow precision loss is 22
|
||||
x = x.times(Math.pow(5, -k));
|
||||
x = taylorSeries(Ctor, 2, x, x);
|
||||
|
||||
// Reverse argument reduction
|
||||
var sin2_x,
|
||||
d5 = new Ctor(5),
|
||||
d16 = new Ctor(16),
|
||||
d20 = new Ctor(20);
|
||||
for (; k--;) {
|
||||
sin2_x = x.times(x);
|
||||
x = x.times(d5.plus(sin2_x.times(d16.times(sin2_x).minus(d20))));
|
||||
}
|
||||
|
||||
return x;
|
||||
}
|
||||
|
||||
|
||||
// Calculate Taylor series for `cos`, `cosh`, `sin` and `sinh`.
|
||||
function taylorSeries(Ctor, n, x, y, isHyperbolic) {
|
||||
var j, t, u, x2,
|
||||
i = 1,
|
||||
pr = Ctor.precision,
|
||||
k = Math.ceil(pr / LOG_BASE);
|
||||
|
||||
external = false;
|
||||
x2 = x.times(x);
|
||||
u = new Ctor(y);
|
||||
|
||||
for (;;) {
|
||||
t = divide(u.times(x2), new Ctor(n++ * n++), pr, 1);
|
||||
u = isHyperbolic ? y.plus(t) : y.minus(t);
|
||||
y = divide(t.times(x2), new Ctor(n++ * n++), pr, 1);
|
||||
t = u.plus(y);
|
||||
|
||||
if (t.d[k] !== void 0) {
|
||||
for (j = k; t.d[j] === u.d[j] && j--;);
|
||||
if (j == -1) break;
|
||||
}
|
||||
|
||||
j = u;
|
||||
u = y;
|
||||
y = t;
|
||||
t = j;
|
||||
i++;
|
||||
}
|
||||
|
||||
external = true;
|
||||
t.d.length = k + 1;
|
||||
|
||||
return t;
|
||||
}
|
||||
|
||||
|
||||
// Return the absolute value of `x` reduced to less than or equal to half pi.
|
||||
function toLessThanHalfPi(Ctor, x) {
|
||||
var t,
|
||||
isNeg = x.s < 0,
|
||||
pi = getPi(Ctor, Ctor.precision, 1),
|
||||
halfPi = pi.times(0.5);
|
||||
|
||||
x = x.abs();
|
||||
|
||||
if (x.lte(halfPi)) {
|
||||
quadrant = isNeg ? 4 : 1;
|
||||
return x;
|
||||
}
|
||||
|
||||
t = x.divToInt(pi);
|
||||
|
||||
if (t.isZero()) {
|
||||
quadrant = isNeg ? 3 : 2;
|
||||
} else {
|
||||
x = x.minus(t.times(pi));
|
||||
|
||||
// 0 <= x < pi
|
||||
if (x.lte(halfPi)) {
|
||||
quadrant = isOdd(t) ? (isNeg ? 2 : 3) : (isNeg ? 4 : 1);
|
||||
return x;
|
||||
}
|
||||
|
||||
quadrant = isOdd(t) ? (isNeg ? 1 : 4) : (isNeg ? 3 : 2);
|
||||
}
|
||||
|
||||
return x.minus(pi).abs();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return the value of Decimal `x` as a string in base `baseOut`.
|
||||
*
|
||||
* If the optional `sd` argument is present include a binary exponent suffix.
|
||||
*/
|
||||
function toStringBinary(x, baseOut, sd, rm) {
|
||||
var base, e, i, k, len, roundUp, str, xd, y,
|
||||
Ctor = x.constructor,
|
||||
isExp = sd !== void 0;
|
||||
|
||||
if (isExp) {
|
||||
checkInt32(sd, 1, MAX_DIGITS);
|
||||
if (rm === void 0) rm = Ctor.rounding;
|
||||
else checkInt32(rm, 0, 8);
|
||||
} else {
|
||||
sd = Ctor.precision;
|
||||
rm = Ctor.rounding;
|
||||
}
|
||||
|
||||
if (!x.isFinite()) {
|
||||
str = nonFiniteToString(x);
|
||||
} else {
|
||||
str = finiteToString(x);
|
||||
i = str.indexOf('.');
|
||||
|
||||
// Use exponential notation according to `toExpPos` and `toExpNeg`? No, but if required:
|
||||
// maxBinaryExponent = floor((decimalExponent + 1) * log[2](10))
|
||||
// minBinaryExponent = floor(decimalExponent * log[2](10))
|
||||
// log[2](10) = 3.321928094887362347870319429489390175864
|
||||
|
||||
if (isExp) {
|
||||
base = 2;
|
||||
if (baseOut == 16) {
|
||||
sd = sd * 4 - 3;
|
||||
} else if (baseOut == 8) {
|
||||
sd = sd * 3 - 2;
|
||||
}
|
||||
} else {
|
||||
base = baseOut;
|
||||
}
|
||||
|
||||
// Convert the number as an integer then divide the result by its base raised to a power such
|
||||
// that the fraction part will be restored.
|
||||
|
||||
// Non-integer.
|
||||
if (i >= 0) {
|
||||
str = str.replace('.', '');
|
||||
y = new Ctor(1);
|
||||
y.e = str.length - i;
|
||||
y.d = convertBase(finiteToString(y), 10, base);
|
||||
y.e = y.d.length;
|
||||
}
|
||||
|
||||
xd = convertBase(str, 10, base);
|
||||
e = len = xd.length;
|
||||
|
||||
// Remove trailing zeros.
|
||||
for (; xd[--len] == 0;) xd.pop();
|
||||
|
||||
if (!xd[0]) {
|
||||
str = isExp ? '0p+0' : '0';
|
||||
} else {
|
||||
if (i < 0) {
|
||||
e--;
|
||||
} else {
|
||||
x = new Ctor(x);
|
||||
x.d = xd;
|
||||
x.e = e;
|
||||
x = divide(x, y, sd, rm, 0, base);
|
||||
xd = x.d;
|
||||
e = x.e;
|
||||
roundUp = inexact;
|
||||
}
|
||||
|
||||
// The rounding digit, i.e. the digit after the digit that may be rounded up.
|
||||
i = xd[sd];
|
||||
k = base / 2;
|
||||
roundUp = roundUp || xd[sd + 1] !== void 0;
|
||||
|
||||
roundUp = rm < 4
|
||||
? (i !== void 0 || roundUp) && (rm === 0 || rm === (x.s < 0 ? 3 : 2))
|
||||
: i > k || i === k && (rm === 4 || roundUp || rm === 6 && xd[sd - 1] & 1 ||
|
||||
rm === (x.s < 0 ? 8 : 7));
|
||||
|
||||
xd.length = sd;
|
||||
|
||||
if (roundUp) {
|
||||
|
||||
// Rounding up may mean the previous digit has to be rounded up and so on.
|
||||
for (; ++xd[--sd] > base - 1;) {
|
||||
xd[sd] = 0;
|
||||
if (!sd) {
|
||||
++e;
|
||||
xd.unshift(1);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// Determine trailing zeros.
|
||||
for (len = xd.length; !xd[len - 1]; --len);
|
||||
|
||||
// E.g. [4, 11, 15] becomes 4bf.
|
||||
for (i = 0, str = ''; i < len; i++) str += NUMERALS.charAt(xd[i]);
|
||||
|
||||
// Add binary exponent suffix?
|
||||
if (isExp) {
|
||||
if (len > 1) {
|
||||
if (baseOut == 16 || baseOut == 8) {
|
||||
i = baseOut == 16 ? 4 : 3;
|
||||
for (--len; len % i; len++) str += '0';
|
||||
xd = convertBase(str, base, baseOut);
|
||||
for (len = xd.length; !xd[len - 1]; --len);
|
||||
|
||||
// xd[0] will always be be 1
|
||||
for (i = 1, str = '1.'; i < len; i++) str += NUMERALS.charAt(xd[i]);
|
||||
} else {
|
||||
str = str.charAt(0) + '.' + str.slice(1);
|
||||
}
|
||||
}
|
||||
|
||||
str = str + (e < 0 ? 'p' : 'p+') + e;
|
||||
} else if (e < 0) {
|
||||
for (; ++e;) str = '0' + str;
|
||||
str = '0.' + str;
|
||||
} else {
|
||||
if (++e > len) for (e -= len; e-- ;) str += '0';
|
||||
else if (e < len) str = str.slice(0, e) + '.' + str.slice(e);
|
||||
}
|
||||
}
|
||||
|
||||
str = (baseOut == 16 ? '0x' : baseOut == 2 ? '0b' : baseOut == 8 ? '0o' : '') + str;
|
||||
}
|
||||
|
||||
return x.s < 0 ? '-' + str : str;
|
||||
}
|
||||
|
||||
|
||||
// Does not strip trailing zeros.
|
||||
function truncate(arr, len) {
|
||||
if (arr.length > len) {
|
||||
arr.length = len;
|
||||
return true;
|
||||
}
|
||||
}
|
||||
|
||||
|
||||
// Decimal methods
|
||||
|
||||
|
||||
/*
|
||||
* abs
|
||||
* acos
|
||||
* acosh
|
||||
* add
|
||||
* asin
|
||||
* asinh
|
||||
* atan
|
||||
* atanh
|
||||
* atan2
|
||||
* cbrt
|
||||
* ceil
|
||||
* clone
|
||||
* config
|
||||
* cos
|
||||
* cosh
|
||||
* div
|
||||
* exp
|
||||
* floor
|
||||
* hypot
|
||||
* ln
|
||||
* log
|
||||
* log2
|
||||
* log10
|
||||
* max
|
||||
* min
|
||||
* mod
|
||||
* mul
|
||||
* pow
|
||||
* random
|
||||
* round
|
||||
* set
|
||||
* sign
|
||||
* sin
|
||||
* sinh
|
||||
* sqrt
|
||||
* sub
|
||||
* tan
|
||||
* tanh
|
||||
* trunc
|
||||
*/
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the absolute value of `x`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function abs(x) {
|
||||
return new this(x).abs();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arccosine in radians of `x`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function acos(x) {
|
||||
return new this(x).acos();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic cosine of `x`, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function acosh(x) {
|
||||
return new this(x).acosh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the sum of `x` and `y`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
* y {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function add(x, y) {
|
||||
return new this(x).plus(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arcsine in radians of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function asin(x) {
|
||||
return new this(x).asin();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic sine of `x`, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function asinh(x) {
|
||||
return new this(x).asinh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arctangent in radians of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function atan(x) {
|
||||
return new this(x).atan();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the inverse of the hyperbolic tangent of `x`, rounded to
|
||||
* `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function atanh(x) {
|
||||
return new this(x).atanh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the arctangent in radians of `y/x` in the range -pi to pi
|
||||
* (inclusive), rounded to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* Domain: [-Infinity, Infinity]
|
||||
* Range: [-pi, pi]
|
||||
*
|
||||
* y {number|string|Decimal} The y-coordinate.
|
||||
* x {number|string|Decimal} The x-coordinate.
|
||||
*
|
||||
* atan2(±0, -0) = ±pi
|
||||
* atan2(±0, +0) = ±0
|
||||
* atan2(±0, -x) = ±pi for x > 0
|
||||
* atan2(±0, x) = ±0 for x > 0
|
||||
* atan2(-y, ±0) = -pi/2 for y > 0
|
||||
* atan2(y, ±0) = pi/2 for y > 0
|
||||
* atan2(±y, -Infinity) = ±pi for finite y > 0
|
||||
* atan2(±y, +Infinity) = ±0 for finite y > 0
|
||||
* atan2(±Infinity, x) = ±pi/2 for finite x
|
||||
* atan2(±Infinity, -Infinity) = ±3*pi/4
|
||||
* atan2(±Infinity, +Infinity) = ±pi/4
|
||||
* atan2(NaN, x) = NaN
|
||||
* atan2(y, NaN) = NaN
|
||||
*
|
||||
*/
|
||||
function atan2(y, x) {
|
||||
y = new this(y);
|
||||
x = new this(x);
|
||||
var r,
|
||||
pr = this.precision,
|
||||
rm = this.rounding,
|
||||
wpr = pr + 4;
|
||||
|
||||
// Either NaN
|
||||
if (!y.s || !x.s) {
|
||||
r = new this(NaN);
|
||||
|
||||
// Both ±Infinity
|
||||
} else if (!y.d && !x.d) {
|
||||
r = getPi(this, wpr, 1).times(x.s > 0 ? 0.25 : 0.75);
|
||||
r.s = y.s;
|
||||
|
||||
// x is ±Infinity or y is ±0
|
||||
} else if (!x.d || y.isZero()) {
|
||||
r = x.s < 0 ? getPi(this, pr, rm) : new this(0);
|
||||
r.s = y.s;
|
||||
|
||||
// y is ±Infinity or x is ±0
|
||||
} else if (!y.d || x.isZero()) {
|
||||
r = getPi(this, wpr, 1).times(0.5);
|
||||
r.s = y.s;
|
||||
|
||||
// Both non-zero and finite
|
||||
} else if (x.s < 0) {
|
||||
this.precision = wpr;
|
||||
this.rounding = 1;
|
||||
r = this.atan(divide(y, x, wpr, 1));
|
||||
x = getPi(this, wpr, 1);
|
||||
this.precision = pr;
|
||||
this.rounding = rm;
|
||||
r = y.s < 0 ? r.minus(x) : r.plus(x);
|
||||
} else {
|
||||
r = this.atan(divide(y, x, wpr, 1));
|
||||
}
|
||||
|
||||
return r;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the cube root of `x`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function cbrt(x) {
|
||||
return new this(x).cbrt();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` rounded to an integer using `ROUND_CEIL`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function ceil(x) {
|
||||
return finalise(x = new this(x), x.e + 1, 2);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Configure global settings for a Decimal constructor.
|
||||
*
|
||||
* `obj` is an object with one or more of the following properties,
|
||||
*
|
||||
* precision {number}
|
||||
* rounding {number}
|
||||
* toExpNeg {number}
|
||||
* toExpPos {number}
|
||||
* maxE {number}
|
||||
* minE {number}
|
||||
* modulo {number}
|
||||
* crypto {boolean|number}
|
||||
*
|
||||
* E.g. Decimal.config({ precision: 20, rounding: 4 })
|
||||
*
|
||||
*/
|
||||
function config(obj) {
|
||||
if (!obj || typeof obj !== 'object') throw Error(decimalError + 'Object expected');
|
||||
var i, p, v,
|
||||
ps = [
|
||||
'precision', 1, MAX_DIGITS,
|
||||
'rounding', 0, 8,
|
||||
'toExpNeg', -EXP_LIMIT, 0,
|
||||
'toExpPos', 0, EXP_LIMIT,
|
||||
'maxE', 0, EXP_LIMIT,
|
||||
'minE', -EXP_LIMIT, 0,
|
||||
'modulo', 0, 9
|
||||
];
|
||||
|
||||
for (i = 0; i < ps.length; i += 3) {
|
||||
if ((v = obj[p = ps[i]]) !== void 0) {
|
||||
if (mathfloor(v) === v && v >= ps[i + 1] && v <= ps[i + 2]) this[p] = v;
|
||||
else throw Error(invalidArgument + p + ': ' + v);
|
||||
}
|
||||
}
|
||||
|
||||
if ((v = obj[p = 'crypto']) !== void 0) {
|
||||
if (v === true || v === false || v === 0 || v === 1) {
|
||||
if (v) {
|
||||
if (typeof crypto != 'undefined' && crypto &&
|
||||
(crypto.getRandomValues || crypto.randomBytes)) {
|
||||
this[p] = true;
|
||||
} else {
|
||||
throw Error(cryptoUnavailable);
|
||||
}
|
||||
} else {
|
||||
this[p] = false;
|
||||
}
|
||||
} else {
|
||||
throw Error(invalidArgument + p + ': ' + v);
|
||||
}
|
||||
}
|
||||
|
||||
return this;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the cosine of `x`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function cos(x) {
|
||||
return new this(x).cos();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic cosine of `x`, rounded to precision
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function cosh(x) {
|
||||
return new this(x).cosh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Create and return a Decimal constructor with the same configuration properties as this Decimal
|
||||
* constructor.
|
||||
*
|
||||
*/
|
||||
function clone(obj) {
|
||||
var i, p, ps;
|
||||
|
||||
/*
|
||||
* The Decimal constructor and exported function.
|
||||
* Return a new Decimal instance.
|
||||
*
|
||||
* v {number|string|Decimal} A numeric value.
|
||||
*
|
||||
*/
|
||||
function Decimal(v) {
|
||||
var e, i, t,
|
||||
x = this;
|
||||
|
||||
// Decimal called without new.
|
||||
if (!(x instanceof Decimal)) return new Decimal(v);
|
||||
|
||||
// Retain a reference to this Decimal constructor, and shadow Decimal.prototype.constructor
|
||||
// which points to Object.
|
||||
x.constructor = Decimal;
|
||||
|
||||
// Duplicate.
|
||||
if (v instanceof Decimal) {
|
||||
x.s = v.s;
|
||||
x.e = v.e;
|
||||
x.d = (v = v.d) ? v.slice() : v;
|
||||
return;
|
||||
}
|
||||
|
||||
t = typeof v;
|
||||
|
||||
if (t === 'number') {
|
||||
if (v === 0) {
|
||||
x.s = 1 / v < 0 ? -1 : 1;
|
||||
x.e = 0;
|
||||
x.d = [0];
|
||||
return;
|
||||
}
|
||||
|
||||
if (v < 0) {
|
||||
v = -v;
|
||||
x.s = -1;
|
||||
} else {
|
||||
x.s = 1;
|
||||
}
|
||||
|
||||
// Fast path for small integers.
|
||||
if (v === ~~v && v < 1e7) {
|
||||
for (e = 0, i = v; i >= 10; i /= 10) e++;
|
||||
x.e = e;
|
||||
x.d = [v];
|
||||
return;
|
||||
|
||||
// Infinity, NaN.
|
||||
} else if (v * 0 !== 0) {
|
||||
if (!v) x.s = NaN;
|
||||
x.e = NaN;
|
||||
x.d = null;
|
||||
return;
|
||||
}
|
||||
|
||||
return parseDecimal(x, v.toString());
|
||||
|
||||
} else if (t !== 'string') {
|
||||
throw Error(invalidArgument + v);
|
||||
}
|
||||
|
||||
// Minus sign?
|
||||
if (v.charCodeAt(0) === 45) {
|
||||
v = v.slice(1);
|
||||
x.s = -1;
|
||||
} else {
|
||||
x.s = 1;
|
||||
}
|
||||
|
||||
return isDecimal.test(v) ? parseDecimal(x, v) : parseOther(x, v);
|
||||
}
|
||||
|
||||
Decimal.prototype = P;
|
||||
|
||||
Decimal.ROUND_UP = 0;
|
||||
Decimal.ROUND_DOWN = 1;
|
||||
Decimal.ROUND_CEIL = 2;
|
||||
Decimal.ROUND_FLOOR = 3;
|
||||
Decimal.ROUND_HALF_UP = 4;
|
||||
Decimal.ROUND_HALF_DOWN = 5;
|
||||
Decimal.ROUND_HALF_EVEN = 6;
|
||||
Decimal.ROUND_HALF_CEIL = 7;
|
||||
Decimal.ROUND_HALF_FLOOR = 8;
|
||||
Decimal.EUCLID = 9;
|
||||
|
||||
Decimal.config = Decimal.set = config;
|
||||
Decimal.clone = clone;
|
||||
|
||||
Decimal.abs = abs;
|
||||
Decimal.acos = acos;
|
||||
Decimal.acosh = acosh; // ES6
|
||||
Decimal.add = add;
|
||||
Decimal.asin = asin;
|
||||
Decimal.asinh = asinh; // ES6
|
||||
Decimal.atan = atan;
|
||||
Decimal.atanh = atanh; // ES6
|
||||
Decimal.atan2 = atan2;
|
||||
Decimal.cbrt = cbrt; // ES6
|
||||
Decimal.ceil = ceil;
|
||||
Decimal.cos = cos;
|
||||
Decimal.cosh = cosh; // ES6
|
||||
Decimal.div = div;
|
||||
Decimal.exp = exp;
|
||||
Decimal.floor = floor;
|
||||
Decimal.hypot = hypot; // ES6
|
||||
Decimal.ln = ln;
|
||||
Decimal.log = log;
|
||||
Decimal.log10 = log10; // ES6
|
||||
Decimal.log2 = log2; // ES6
|
||||
Decimal.max = max;
|
||||
Decimal.min = min;
|
||||
Decimal.mod = mod;
|
||||
Decimal.mul = mul;
|
||||
Decimal.pow = pow;
|
||||
Decimal.random = random;
|
||||
Decimal.round = round;
|
||||
Decimal.sign = sign; // ES6
|
||||
Decimal.sin = sin;
|
||||
Decimal.sinh = sinh; // ES6
|
||||
Decimal.sqrt = sqrt;
|
||||
Decimal.sub = sub;
|
||||
Decimal.tan = tan;
|
||||
Decimal.tanh = tanh; // ES6
|
||||
Decimal.trunc = trunc; // ES6
|
||||
|
||||
if (obj === void 0) obj = {};
|
||||
if (obj) {
|
||||
ps = ['precision', 'rounding', 'toExpNeg', 'toExpPos', 'maxE', 'minE', 'modulo', 'crypto'];
|
||||
for (i = 0; i < ps.length;) if (!obj.hasOwnProperty(p = ps[i++])) obj[p] = this[p];
|
||||
}
|
||||
|
||||
Decimal.config(obj);
|
||||
|
||||
return Decimal;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` divided by `y`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
* y {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function div(x, y) {
|
||||
return new this(x).div(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural exponential of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} The power to which to raise the base of the natural log.
|
||||
*
|
||||
*/
|
||||
function exp(x) {
|
||||
return new this(x).exp();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` round to an integer using `ROUND_FLOOR`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function floor(x) {
|
||||
return finalise(x = new this(x), x.e + 1, 3);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the square root of the sum of the squares of the arguments,
|
||||
* rounded to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* hypot(a, b, ...) = sqrt(a^2 + b^2 + ...)
|
||||
*
|
||||
*/
|
||||
function hypot() {
|
||||
var i, n,
|
||||
t = new this(0);
|
||||
|
||||
external = false;
|
||||
|
||||
for (i = 0; i < arguments.length;) {
|
||||
n = new this(arguments[i++]);
|
||||
if (!n.d) {
|
||||
if (n.s) {
|
||||
external = true;
|
||||
return new this(1 / 0);
|
||||
}
|
||||
t = n;
|
||||
} else if (t.d) {
|
||||
t = t.plus(n.times(n));
|
||||
}
|
||||
}
|
||||
|
||||
external = true;
|
||||
|
||||
return t.sqrt();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the natural logarithm of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function ln(x) {
|
||||
return new this(x).ln();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the log of `x` to the base `y`, or to base 10 if no base
|
||||
* is specified, rounded to `precision` significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* log[y](x)
|
||||
*
|
||||
* x {number|string|Decimal} The argument of the logarithm.
|
||||
* y {number|string|Decimal} The base of the logarithm.
|
||||
*
|
||||
*/
|
||||
function log(x, y) {
|
||||
return new this(x).log(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the base 2 logarithm of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function log2(x) {
|
||||
return new this(x).log(2);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the base 10 logarithm of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function log10(x) {
|
||||
return new this(x).log(10);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the maximum of the arguments.
|
||||
*
|
||||
* arguments {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function max() {
|
||||
return maxOrMin(this, arguments, 'lt');
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the minimum of the arguments.
|
||||
*
|
||||
* arguments {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function min() {
|
||||
return maxOrMin(this, arguments, 'gt');
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` modulo `y`, rounded to `precision` significant digits
|
||||
* using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
* y {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function mod(x, y) {
|
||||
return new this(x).mod(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` multiplied by `y`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
* y {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function mul(x, y) {
|
||||
return new this(x).mul(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` raised to the power `y`, rounded to precision
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} The base.
|
||||
* y {number|string|Decimal} The exponent.
|
||||
*
|
||||
*/
|
||||
function pow(x, y) {
|
||||
return new this(x).pow(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Returns a new Decimal with a random value equal to or greater than 0 and less than 1, and with
|
||||
* `sd`, or `Decimal.precision` if `sd` is omitted, significant digits (or less if trailing zeros
|
||||
* are produced).
|
||||
*
|
||||
* [sd] {number} Significant digits. Integer, 0 to MAX_DIGITS inclusive.
|
||||
*
|
||||
*/
|
||||
function random(sd) {
|
||||
var d, e, k, n,
|
||||
i = 0,
|
||||
r = new this(1),
|
||||
rd = [];
|
||||
|
||||
if (sd === void 0) sd = this.precision;
|
||||
else checkInt32(sd, 1, MAX_DIGITS);
|
||||
|
||||
k = Math.ceil(sd / LOG_BASE);
|
||||
|
||||
if (!this.crypto) {
|
||||
for (; i < k;) rd[i++] = Math.random() * 1e7 | 0;
|
||||
|
||||
// Browsers supporting crypto.getRandomValues.
|
||||
} else if (crypto.getRandomValues) {
|
||||
d = crypto.getRandomValues(new Uint32Array(k));
|
||||
|
||||
for (; i < k;) {
|
||||
n = d[i];
|
||||
|
||||
// 0 <= n < 4294967296
|
||||
// Probability n >= 4.29e9, is 4967296 / 4294967296 = 0.00116 (1 in 865).
|
||||
if (n >= 4.29e9) {
|
||||
d[i] = crypto.getRandomValues(new Uint32Array(1))[0];
|
||||
} else {
|
||||
|
||||
// 0 <= n <= 4289999999
|
||||
// 0 <= (n % 1e7) <= 9999999
|
||||
rd[i++] = n % 1e7;
|
||||
}
|
||||
}
|
||||
|
||||
// Node.js supporting crypto.randomBytes.
|
||||
} else if (crypto.randomBytes) {
|
||||
|
||||
// buffer
|
||||
d = crypto.randomBytes(k *= 4);
|
||||
|
||||
for (; i < k;) {
|
||||
|
||||
// 0 <= n < 2147483648
|
||||
n = d[i] + (d[i + 1] << 8) + (d[i + 2] << 16) + ((d[i + 3] & 0x7f) << 24);
|
||||
|
||||
// Probability n >= 2.14e9, is 7483648 / 2147483648 = 0.0035 (1 in 286).
|
||||
if (n >= 2.14e9) {
|
||||
crypto.randomBytes(4).copy(d, i);
|
||||
} else {
|
||||
|
||||
// 0 <= n <= 2139999999
|
||||
// 0 <= (n % 1e7) <= 9999999
|
||||
rd.push(n % 1e7);
|
||||
i += 4;
|
||||
}
|
||||
}
|
||||
|
||||
i = k / 4;
|
||||
} else {
|
||||
throw Error(cryptoUnavailable);
|
||||
}
|
||||
|
||||
k = rd[--i];
|
||||
sd %= LOG_BASE;
|
||||
|
||||
// Convert trailing digits to zeros according to sd.
|
||||
if (k && sd) {
|
||||
n = mathpow(10, LOG_BASE - sd);
|
||||
rd[i] = (k / n | 0) * n;
|
||||
}
|
||||
|
||||
// Remove trailing words which are zero.
|
||||
for (; rd[i] === 0; i--) rd.pop();
|
||||
|
||||
// Zero?
|
||||
if (i < 0) {
|
||||
e = 0;
|
||||
rd = [0];
|
||||
} else {
|
||||
e = -1;
|
||||
|
||||
// Remove leading words which are zero and adjust exponent accordingly.
|
||||
for (; rd[0] === 0; e -= LOG_BASE) rd.shift();
|
||||
|
||||
// Count the digits of the first word of rd to determine leading zeros.
|
||||
for (k = 1, n = rd[0]; n >= 10; n /= 10) k++;
|
||||
|
||||
// Adjust the exponent for leading zeros of the first word of rd.
|
||||
if (k < LOG_BASE) e -= LOG_BASE - k;
|
||||
}
|
||||
|
||||
r.e = e;
|
||||
r.d = rd;
|
||||
|
||||
return r;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` rounded to an integer using rounding mode `rounding`.
|
||||
*
|
||||
* To emulate `Math.round`, set rounding to 7 (ROUND_HALF_CEIL).
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function round(x) {
|
||||
return finalise(x = new this(x), x.e + 1, this.rounding);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return
|
||||
* 1 if x > 0,
|
||||
* -1 if x < 0,
|
||||
* 0 if x is 0,
|
||||
* -0 if x is -0,
|
||||
* NaN otherwise
|
||||
*
|
||||
*/
|
||||
function sign(x) {
|
||||
x = new this(x);
|
||||
return x.d ? (x.d[0] ? x.s : 0 * x.s) : x.s || NaN;
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the sine of `x`, rounded to `precision` significant digits
|
||||
* using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function sin(x) {
|
||||
return new this(x).sin();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic sine of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function sinh(x) {
|
||||
return new this(x).sinh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the square root of `x`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function sqrt(x) {
|
||||
return new this(x).sqrt();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` minus `y`, rounded to `precision` significant digits
|
||||
* using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
* y {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function sub(x, y) {
|
||||
return new this(x).sub(y);
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the tangent of `x`, rounded to `precision` significant
|
||||
* digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function tan(x) {
|
||||
return new this(x).tan();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is the hyperbolic tangent of `x`, rounded to `precision`
|
||||
* significant digits using rounding mode `rounding`.
|
||||
*
|
||||
* x {number|string|Decimal} A value in radians.
|
||||
*
|
||||
*/
|
||||
function tanh(x) {
|
||||
return new this(x).tanh();
|
||||
}
|
||||
|
||||
|
||||
/*
|
||||
* Return a new Decimal whose value is `x` truncated to an integer.
|
||||
*
|
||||
* x {number|string|Decimal}
|
||||
*
|
||||
*/
|
||||
function trunc(x) {
|
||||
return finalise(x = new this(x), x.e + 1, 1);
|
||||
}
|
||||
|
||||
|
||||
// Create and configure initial Decimal constructor.
|
||||
Decimal = clone(Decimal);
|
||||
|
||||
// Create the internal constants from their string values.
|
||||
LN10 = new Decimal(LN10);
|
||||
PI = new Decimal(PI);
|
||||
|
||||
|
||||
// Export.
|
||||
|
||||
|
||||
// AMD.
|
||||
if (typeof define == 'function' && define.amd) {
|
||||
define(function () {
|
||||
return Decimal;
|
||||
});
|
||||
|
||||
// Node and other environments that support module.exports.
|
||||
} else if (typeof module != 'undefined' && module.exports) {
|
||||
module.exports = Decimal.default = Decimal.Decimal = Decimal;
|
||||
|
||||
// Browser.
|
||||
} else {
|
||||
if (!globalScope) {
|
||||
globalScope = typeof self != 'undefined' && self && self.self == self
|
||||
? self : Function('return this')();
|
||||
}
|
||||
|
||||
noConflict = globalScope.Decimal;
|
||||
Decimal.noConflict = function () {
|
||||
globalScope.Decimal = noConflict;
|
||||
return Decimal;
|
||||
};
|
||||
|
||||
globalScope.Decimal = Decimal;
|
||||
}
|
||||
})(this);
|
||||
3
nodered/rootfs/data/node_modules/decimal.js/decimal.min.js
generated
vendored
Normal file
3
nodered/rootfs/data/node_modules/decimal.js/decimal.min.js
generated
vendored
Normal file
File diff suppressed because one or more lines are too long
2629
nodered/rootfs/data/node_modules/decimal.js/doc/API.html
generated
vendored
Normal file
2629
nodered/rootfs/data/node_modules/decimal.js/doc/API.html
generated
vendored
Normal file
@@ -0,0 +1,2629 @@
|
||||
<!DOCTYPE HTML>
|
||||
<html>
|
||||
<head>
|
||||
<meta charset="utf-8">
|
||||
<meta http-equiv="X-UA-Compatible" content="IE=edge">
|
||||
<meta name="Author" content="MMclaughlin">
|
||||
<title>decimal.js API</title>
|
||||
<style>
|
||||
html{font-size:100%}
|
||||
body{background:#fff;font-family:"Helvetica Neue",Helvetica,Arial,sans-serif;font-size:13px;
|
||||
line-height:1.65em;min-height:100%;margin:0}
|
||||
body,i{color:#000}
|
||||
.nav{background:#fff;position:fixed;top:0;bottom:0;left:0;width:210px;overflow-y:auto;
|
||||
padding:15px 0 30px 15px}
|
||||
div.container{width:600px;margin:50px 0 50px 240px}
|
||||
p{margin:0 0 1em;width:600px}
|
||||
pre,ul{margin:1em 0}
|
||||
h1,h2,h3,h4,h5{margin:0;padding:1.5em 0 0}
|
||||
h1,h2{padding:.75em 0}
|
||||
h1{font:400 3em Consolas, monaco, monospace;color:#000;margin-bottom:1em}
|
||||
h2{font-size:2.25em;color:#f00}
|
||||
h3{font-size:1.75em;color:#69d2e7}
|
||||
h4{font-size:1.75em;color:#f00;padding-bottom:.75em}
|
||||
h5{font-size:1.2em;margin-bottom:.4em}
|
||||
h6{font-size:1.1em;margin-bottom:0.8em;padding:0.5em 0}
|
||||
dd dt{font-size:1.2em}
|
||||
dt{padding-top:.5em}
|
||||
dd{padding-top:.35em}
|
||||
b{font-weight:700}
|
||||
a,a:visited{color:#f00;text-decoration:none}
|
||||
a:active,a:hover{outline:0;text-decoration:underline}
|
||||
.nav a,.nav b,.nav a:visited{display:block;color:#f00;font-weight:700;margin-top:15px}
|
||||
.nav b{color:#69d2e7;margin-top:20px;cursor:default;width:auto}
|
||||
ul{list-style-type:none;padding:0 0 0 20px}
|
||||
.nav ul{line-height:14px;padding-left:0;margin:5px 0 0}
|
||||
.nav ul a,.nav ul a:visited,span{display:inline;color:#000;font-family:Verdana,Geneva,sans-serif;
|
||||
font-size:11px;font-weight:400;margin:0}
|
||||
.inset{margin-left:20px;font-size:.9em}
|
||||
.nav li{width:auto;margin:0 0 3px}
|
||||
.alias{font-style:italic;margin-left:20px}
|
||||
table{border-collapse:collapse;border-spacing:0;border:2px solid #a7dbd8;margin:1.75em 0;padding:0}
|
||||
td,th{text-align:left;margin:0;padding:2px 5px;border:1px dotted #a7dbd8}
|
||||
th{border-top:2px solid #a7dbd8;border-bottom:2px solid #a7dbd8;color:#f00}
|
||||
code,pre{font-family:Consolas, monaco, monospace;font-weight:400}
|
||||
pre{background:#f5f5f5;white-space:pre-wrap;word-wrap:break-word;border-left:5px solid #a7dbd8;
|
||||
padding:1px 0 1px 15px;margin:1.2em 0}
|
||||
code,.nav-title{color:#f00}
|
||||
.end{margin-bottom:25px}
|
||||
.centre{text-align:center}
|
||||
#modes,#configProps{color:#f00}
|
||||
.spacer{line-height:0px}
|
||||
#faq{margin:3em 0 0}
|
||||
li span{float:right;margin-right:10px;color:#c0c0c0}
|
||||
#js{font:inherit;color:#f00}
|
||||
</style>
|
||||
</head>
|
||||
<body>
|
||||
|
||||
<div class="nav">
|
||||
|
||||
<a class='nav-title' href="#">API</a>
|
||||
|
||||
<b>CONSTRUCTOR</b>
|
||||
<ul><li><a href="#decimal"><strong>Decimal</strong></a></li></ul>
|
||||
|
||||
<a href="#methods">Methods</a>
|
||||
<ul>
|
||||
<li><a href="#Dabs" >abs</a></li>
|
||||
<li><a href="#Dacos" >acos</a></li>
|
||||
<li><a href="#Dacosh" >acosh</a></li>
|
||||
<li><a href="#Dadd" >add</a></li>
|
||||
<li><a href="#Dasin" >asin</a></li>
|
||||
<li><a href="#Dasinh" >asinh</a></li>
|
||||
<li><a href="#Datan" >atan</a></li>
|
||||
<li><a href="#Datanh" >atanh</a></li>
|
||||
<li><a href="#Datan2" >atan2</a></li>
|
||||
<li><a href="#Dcbrt" >cbrt</a></li>
|
||||
<li><a href="#Dceil" >ceil</a></li>
|
||||
<li><a href="#Dclone" ><strong>clone</strong></a></li>
|
||||
<li><a href="#Dcos" >cos</a></li>
|
||||
<li><a href="#Dcosh" >cosh</a></li>
|
||||
<li><a href="#Ddiv" >div</a></li>
|
||||
<li><a href="#Dexp" >exp</a></li>
|
||||
<li><a href="#Dfloor" >floor</a></li>
|
||||
<li><a href="#Dhypot" >hypot</a></li>
|
||||
<li><a href="#Dln" >ln</a></li>
|
||||
<li><a href="#Dlog" >log</a></li>
|
||||
<li><a href="#Dlog2" >log2</a></li>
|
||||
<li><a href="#Dlog10" >log10</a></li>
|
||||
<li><a href="#Dmax" >max</a></li>
|
||||
<li><a href="#Dmin" >min</a></li>
|
||||
<li><a href="#Dmod" >mod</a></li>
|
||||
<li><a href="#Dmul" >mul</a></li>
|
||||
<li><a href="#DnoConflict"><strong>noConflict</strong></a></li>
|
||||
<li><a href="#Dpow" >pow</a></li>
|
||||
<li><a href="#Drandom" >random</a></li>
|
||||
<li><a href="#Dround" >round</a></li>
|
||||
<li><a href="#Dset" ><strong>set</strong></a></li>
|
||||
<li><a href="#Dsign" >sign</a></li>
|
||||
<li><a href="#Dsin" >sin</a></li>
|
||||
<li><a href="#Dsinh" >sinh</a></li>
|
||||
<li><a href="#Dsqrt" >sqrt</a></li>
|
||||
<li><a href="#Dsub" >sub</a></li>
|
||||
<li><a href="#Dtan" >tan</a></li>
|
||||
<li><a href="#Dtanh" >tanh</a></li>
|
||||
<li><a href="#Dtrunc" >trunc</a></li>
|
||||
</ul>
|
||||
|
||||
<a href="#constructor-properties">Properties</a>
|
||||
<ul>
|
||||
<li><a href="#precision">precision</a></li>
|
||||
<li><a href="#rounding" >rounding</a></li>
|
||||
<li><a href="#minE" >minE</a></li>
|
||||
<li><a href="#maxE" >maxE</a></li>
|
||||
<li><a href="#toExpNeg" >toExpNeg</a></li>
|
||||
<li><a href="#toExpPos" >toExpPos</a></li>
|
||||
<li><a href="#modulo" >modulo</a></li>
|
||||
<li><a href="#crypto" >crypto</a></li>
|
||||
<li class='spacer'> </li>
|
||||
<li><a href="#modes">ROUND_UP</a></li>
|
||||
<li><a href="#modes">ROUND_DOWN</a></li>
|
||||
<li><a href="#modes">ROUND_CEIL</a></li>
|
||||
<li><a href="#modes">ROUND_FLOOR</a></li>
|
||||
<li><a href="#modes">ROUND_HALF_UP</a></li>
|
||||
<li><a href="#modes">ROUND_HALF_DOWN</a></li>
|
||||
<li><a href="#modes">ROUND_HALF_EVEN</a></li>
|
||||
<li><a href="#modes">ROUND_HALF_CEIL</a></li>
|
||||
<li><a href="#modes">ROUND_HALF_FLOOR</a></li>
|
||||
<li><a href="#modes">EUCLID</a></li>
|
||||
</ul>
|
||||
|
||||
<b> INSTANCE </b>
|
||||
|
||||
<a href="#prototype-methods">Methods</a>
|
||||
<ul>
|
||||
<li><a href="#abs" >absoluteValue </a><span>abs</span> </li>
|
||||
<li><a href="#ceil" >ceil </a> </li>
|
||||
<li><a href="#cmp" >comparedTo </a><span>cmp</span> </li>
|
||||
<li><a href="#cos" >cosine </a><span>cos</span> </li>
|
||||
<li><a href="#cbrt" >cubeRoot </a><span>cbrt</span> </li>
|
||||
<li><a href="#dp" >decimalPlaces </a><span>dp</span> </li>
|
||||
<li><a href="#div" >dividedBy </a><span>div</span> </li>
|
||||
<li><a href="#divToInt" >dividedToIntegerBy </a><span>divToInt</span></li>
|
||||
<li><a href="#eq" >equals </a><span>eq</span> </li>
|
||||
<li><a href="#floor" >floor </a> </li>
|
||||
<li><a href="#gt" >greaterThan </a><span>gt</span> </li>
|
||||
<li><a href="#gte" >greaterThanOrEqualTo </a><span>gte</span> </li>
|
||||
<li><a href="#cosh" >hyperbolicCosine </a><span>cosh</span> </li>
|
||||
<li><a href="#sinh" >hyperbolicSine </a><span>sinh</span> </li>
|
||||
<li><a href="#tanh" >hyperbolicTangent </a><span>tanh</span> </li>
|
||||
<li><a href="#acos" >inverseCosine </a><span>acos</span> </li>
|
||||
<li><a href="#acosh" >inverseHyperbolicCosine </a><span>acosh</span> </li>
|
||||
<li><a href="#asinh" >inverseHyperbolicSine </a><span>asinh</span> </li>
|
||||
<li><a href="#atanh" >inverseHyperbolicTangent</a><span>atanh</span> </li>
|
||||
<li><a href="#asin" >inverseSine </a><span>asin</span> </li>
|
||||
<li><a href="#atan" >inverseTangent </a><span>atan</span> </li>
|
||||
<li><a href="#isFinite" >isFinite </a> </li>
|
||||
<li><a href="#isInt" >isInteger </a><span>isInt</span> </li>
|
||||
<li><a href="#isNaN" >isNaN </a> </li>
|
||||
<li><a href="#isNeg" >isNegative </a><span>isNeg</span> </li>
|
||||
<li><a href="#isPos" >isPositive </a><span>isPos</span> </li>
|
||||
<li><a href="#isZero" >isZero </a> </li>
|
||||
<li><a href="#lt" >lessThan </a><span>lt</span> </li>
|
||||
<li><a href="#lte" >lessThanOrEqualTo </a><span>lte</span> </li>
|
||||
<li><a href="#log" >logarithm </a><span>log</span> </li>
|
||||
<li><a href="#sub" >minus </a><span>sub</span> </li>
|
||||
<li><a href="#mod" >modulo </a><span>mod</span> </li>
|
||||
<li><a href="#exp" >naturalExponential </a><span>exp</span> </li>
|
||||
<li><a href="#ln" >naturalLogarithm </a><span>ln</span> </li>
|
||||
<li><a href="#neg" >negated </a><span>neg</span> </li>
|
||||
<li><a href="#add" >plus </a><span>add</span> </li>
|
||||
<li><a href="#sd" >precision </a><span>sd</span> </li>
|
||||
<li><a href="#round" >round </a> </li>
|
||||
<li><a href="#sin" >sine </a><span>sin</span> </li>
|
||||
<li><a href="#sqrt" >squareRoot </a><span>sqrt</span> </li>
|
||||
<li><a href="#tan" >tangent </a><span>tan</span> </li>
|
||||
<li><a href="#mul" >times </a><span>mul</span> </li>
|
||||
<li><a href="#toBinary" >toBinary </a> </li>
|
||||
<li><a href="#toDP" >toDecimalPlaces </a><span>toDP</span> </li>
|
||||
<li><a href="#toExponential">toExponential </a> </li>
|
||||
<li><a href="#toFixed" >toFixed </a> </li>
|
||||
<li><a href="#toFraction" >toFraction </a> </li>
|
||||
<li><a href="#toHex" >toHexadecimal </a><span>toHex</span> </li>
|
||||
<li><a href="#toJSON" >toJSON </a> </li>
|
||||
<li><a href="#toNearest" >toNearest </a> </li>
|
||||
<li><a href="#toNumber" >toNumber </a> </li>
|
||||
<li><a href="#toOctal" >toOctal </a> </li>
|
||||
<li><a href="#pow" >toPower </a><span>pow</span> </li>
|
||||
<li><a href="#toPrecision" >toPrecision </a> </li>
|
||||
<li><a href="#toSD" >toSignificantDigits </a><span>toSD</span> </li>
|
||||
<li><a href="#toString" >toString </a> </li>
|
||||
<li><a href="#trunc" >truncated </a><span>trunc</span> </li>
|
||||
<li><a href="#valueOf" >valueOf </a> </li>
|
||||
</ul>
|
||||
|
||||
<a href="#instance-properties">Properties</a>
|
||||
<ul>
|
||||
<li><a href="#digits" >d</a><span>digits</span></li>
|
||||
<li><a href="#exponent">e</a><span>exponent</span></li>
|
||||
<li><a href="#sign" >s</a><span>sign</span></li>
|
||||
</ul>
|
||||
|
||||
<a href="#zero-nan-infinity">Zero, NaN & Infinity</a>
|
||||
<a href="#Errors">Errors</a>
|
||||
<a href="#Pi">Pi</a>
|
||||
<a class='end' href="#faq">FAQ</a>
|
||||
|
||||
</div>
|
||||
|
||||
<div class="container">
|
||||
|
||||
<h1>decimal<span id='js'>.js</span></h1>
|
||||
|
||||
<p>An arbitrary-precision Decimal type for JavaScript.</p>
|
||||
<p><a href='https://github.com/MikeMcl/decimal.js'>Hosted on GitHub</a>.</p>
|
||||
|
||||
<h2>API</h2>
|
||||
|
||||
<p>
|
||||
See the <a href='https://github.com/MikeMcl/decimal.js'>README</a> on GitHub for a quick-start
|
||||
introduction.
|
||||
</p>
|
||||
<p>
|
||||
In all examples below, <code>var</code> and semicolons are not shown, and if a commented-out
|
||||
value is in quotes it means <code>toString</code> has been called on the preceding expression.
|
||||
</p><br />
|
||||
<p>
|
||||
When the library is loaded, it defines a single function object,
|
||||
<a href='#decimal'><code>Decimal</code></a>, the constructor of Decimal instances.
|
||||
</p>
|
||||
<p>
|
||||
<i>
|
||||
If necessary, multiple Decimal constructors can be created, each with their own independent
|
||||
configuration, e.g. precision and range, which applies to all Decimal instances created from
|
||||
it.
|
||||
</i>
|
||||
</p>
|
||||
<p>
|
||||
<i>
|
||||
A new Decimal constructor is created by calling the <code><a href='#Dclone'>clone</a></code>
|
||||
method of an already existing Decimal constructor.
|
||||
</i>
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h3 class='end'>CONSTRUCTOR</h3>
|
||||
|
||||
<h5 id="decimal">
|
||||
Decimal<code class='inset'>Decimal(value) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<dl>
|
||||
<dt><code>value</code>: <i>number|string|Decimal</i></dt>
|
||||
<dd>
|
||||
A legitimate <code>value</code> is an integer or float, including <code>±0</code>, or
|
||||
is <code>±Infinity</code>, or <code>NaN</code>.
|
||||
</dd>
|
||||
<dd>
|
||||
The number of digits of <code>value</code> is not limited, except by JavaScript's maximum
|
||||
array size and, in practice, the processing time required.
|
||||
</dd>
|
||||
<dd>
|
||||
The allowable range of <code>value</code> is defined in terms of a maximum exponent, see
|
||||
<a href='#maxE'>maxE</a>, and a minimum exponent, see <a href='#minE'>minE</a>.
|
||||
</dd>
|
||||
<dd>
|
||||
As well as in decimal, a string <code>value</code> may be expressed in binary, hexadecimal
|
||||
or octal, if the appropriate prefix is included: <code>0x</code> or <code>0X</code> for
|
||||
hexadecimal, <code>0b</code> or <code>0B</code> for binary, and <code>0o</code> or
|
||||
<code>0O</code> for octal.
|
||||
</dd>
|
||||
<dd>
|
||||
Both decimal and non-decimal string values may use exponential (floating-point), as well as
|
||||
normal (fixed-point) notation.
|
||||
</dd>
|
||||
<dd>
|
||||
In exponential notation, <code>e</code> or <code>E</code> defines a power-of-ten exponent
|
||||
for decimal values, and <code>p</code> or <code>P</code> defines a power-of-two exponent for
|
||||
non-decimal values, i.e. binary, hexadecimal or octal.
|
||||
</dd>
|
||||
</dl>
|
||||
<p>Returns a new Decimal object instance.</p>
|
||||
<p>Throws on an invalid <code>value</code>.</p>
|
||||
<pre>
|
||||
x = new Decimal(9) // '9'
|
||||
y = new Decimal(x) // '9'
|
||||
|
||||
new Decimal('5032485723458348569331745.33434346346912144534543')
|
||||
new Decimal('4.321e+4') // '43210'
|
||||
new Decimal('-735.0918e-430') // '-7.350918e-428'
|
||||
new Decimal('5.6700000') // '5.67'
|
||||
new Decimal(Infinity) // 'Infinity'
|
||||
new Decimal(NaN) // 'NaN'
|
||||
new Decimal('.5') // '0.5'
|
||||
new Decimal('-0b10110100.1') // '-180.5'
|
||||
new Decimal('0xff.8') // '255.5'
|
||||
|
||||
new Decimal(0.046875) // '0.046875'
|
||||
new Decimal('0.046875000000') // '0.046875'
|
||||
|
||||
new Decimal(4.6875e-2) // '0.046875'
|
||||
new Decimal('468.75e-4') // '0.046875'
|
||||
|
||||
new Decimal('0b0.000011') // '0.046875'
|
||||
new Decimal('0o0.03') // '0.046875'
|
||||
new Decimal('0x0.0c') // '0.046875'
|
||||
|
||||
new Decimal('0b1.1p-5') // '0.046875'
|
||||
new Decimal('0o1.4p-5') // '0.046875'
|
||||
new Decimal('0x1.8p-5') // '0.046875'</pre>
|
||||
|
||||
|
||||
|
||||
<h4 id="methods">Methods</h4>
|
||||
<p>The methods of a Decimal constructor.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dabs">abs<code class='inset'>.abs(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#abs'>absoluteValue</a></code>.</p>
|
||||
<pre>a = Decimal.abs(x)
|
||||
b = new Decimal(x).abs()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dacos">acos<code class='inset'>.acos(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#acos'>inverseCosine</a></code>.</p>
|
||||
<pre>a = Decimal.acos(x)
|
||||
b = new Decimal(x).acos()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dacosh">acosh<code class='inset'>.acosh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#acos'>inverseHyperbolicCosine</a></code>.</p>
|
||||
<pre>a = Decimal.acosh(x)
|
||||
b = new Decimal(x).acosh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dadd">add<code class='inset'>.add(x, y) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#add'>plus</a></code>.</p>
|
||||
<pre>a = Decimal.add(x, y)
|
||||
b = new Decimal(x).plus(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dasin">asin<code class='inset'>.asin(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#asin'>inverseSine</a></code>.</p>
|
||||
<pre>a = Decimal.asin(x)
|
||||
b = new Decimal(x).asin()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dasinh">asinh<code class='inset'>.asinh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#asin'>inverseHyperbolicSine</a></code>.</p>
|
||||
<pre>a = Decimal.asinh(x)
|
||||
b = new Decimal(x).asinh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Datan">atan<code class='inset'>.atan(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#atan'>inverseTangent</a></code>.</p>
|
||||
<pre>a = Decimal.atan(x)
|
||||
b = new Decimal(x).atan()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Datanh">atanh<code class='inset'>.atanh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#atan'>inverseHyperbolicTangent</a></code>.</p>
|
||||
<pre>a = Decimal.atanh(x)
|
||||
b = new Decimal(x).atanh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Datan2">atan2<code class='inset'>.atan2(y, x) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>y</code>: <i>number|string|Decimal</i><br />
|
||||
<code>x</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse tangent in radians of the quotient of
|
||||
<code>y</code> and <code>x</code>, rounded to <a href='#precision'><code>precision</code></a>
|
||||
significant digits using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The signs of <code>y</code> and <code>x</code> are used to determine the quadrant of the
|
||||
result.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-pi, pi</code>]
|
||||
</p>
|
||||
<p>
|
||||
See <a href='#Pi'><code>Pi</code></a> and
|
||||
<a href='https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Math/atan2'><code>Math.atan2()</code>.</a>
|
||||
</p>
|
||||
<pre>r = Decimal.atan2(y, x)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dcbrt">cbrt<code class='inset'>.cbrt(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#cbrt'>cubeRoot</a></code>.</p>
|
||||
<pre>a = Decimal.cbrt(x)
|
||||
b = new Decimal(x).cbrt()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dceil">ceil<code class='inset'>.ceil(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#ceil'>ceil</a></code>.</p>
|
||||
<pre>a = Decimal.ceil(x)
|
||||
b = new Decimal(x).ceil()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dclone">
|
||||
clone
|
||||
<code class='inset'>.clone([object]) <i>⇒ Decimal constructor</i></code>
|
||||
</h5>
|
||||
<p><code>object</code>: <i>object</i></p>
|
||||
<p>
|
||||
Returns a new independent Decimal constructor with configuration settings as described by
|
||||
<code>object</code> (see <a href='#Dset'><code>set</code></a>), or with the same
|
||||
settings as <code>this</code> Decimal constructor if <code>object</code> is omitted.
|
||||
</p>
|
||||
<pre>Decimal.set({ precision: 5 })
|
||||
D9 = Decimal.clone({ precision: 9 })
|
||||
|
||||
a = new Decimal(1)
|
||||
b = new D9(1)
|
||||
|
||||
a.div(3) // 0.33333
|
||||
b.div(3) // 0.333333333
|
||||
|
||||
// D9 = Decimal.clone({ precision: 9 }) is equivalent to:
|
||||
D9 = Decimal.clone()
|
||||
D9.set({ precision: 9 })</pre>
|
||||
<p>
|
||||
It is not inefficient in terms of memory usage to use multiple Decimal constructors as
|
||||
functions are shared between them.
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dcos">cos<code class='inset'>.cos(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#cos'>cosine</a></code>.</p>
|
||||
<pre>a = Decimal.cos(x)
|
||||
b = new Decimal(x).cos()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dcosh">cosh<code class='inset'>.cosh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#cos'>hyperbolicCosine</a></code>.</p>
|
||||
<pre>a = Decimal.cosh(x)
|
||||
b = new Decimal(x).cosh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Ddiv">div<code class='inset'>.div(x, y) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#div'>dividedBy</a></code>.</p>
|
||||
<pre>a = Decimal.div(x, y)
|
||||
b = new Decimal(x).div(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dexp">exp<code class='inset'>.exp(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#exp'>naturalExponential</a></code>.</p>
|
||||
<pre>a = Decimal.exp(x)
|
||||
b = new Decimal(x).exp()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dfloor">floor<code class='inset'>.floor(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#floor'>floor</a></code>.</p>
|
||||
<pre>a = Decimal.floor(x)
|
||||
b = new Decimal(x).floor()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dhypot">
|
||||
hypot<code class='inset'>.hypot([x [, y, ...]]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the square root of the sum of the squares of the
|
||||
arguments, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>r = Decimal.hypot(x, y)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dln">ln<code class='inset'>.ln(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#ln'>naturalLogarithm</a></code>.</p>
|
||||
<pre>a = Decimal.ln(x)
|
||||
b = new Decimal(x).ln()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dlog">log<code class='inset'>.log(x [, base]) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>base</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#log'>logarithm</a></code>.</p>
|
||||
<p>
|
||||
The default base is <code>10</code>, which is not the same as JavaScript's
|
||||
<code>Math.log()</code>, which returns the natural logarithm (base <code>e</code>).
|
||||
</p>
|
||||
<pre>a = Decimal.log(x, y)
|
||||
b = new Decimal(x).log(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dlog2">log2<code class='inset'>.log2(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the base <code>2</code> logarithm of <code>x</code>,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>r = Decimal.log2(x)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dlog10">log10<code class='inset'>.log10(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the base <code>10</code> logarithm of <code>x</code>,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>r = Decimal.log10(x)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dmax">
|
||||
max<code class='inset'>.max([x [, y, ...]]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>Returns a new Decimal whose value is the maximum of the <code>arguments</code>.</p>
|
||||
<pre>r = Decimal.max(x, y, z)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dmin">
|
||||
min<code class='inset'>.min([x [, y, ...]]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>Returns a new Decimal whose value is the minimum of the <code>arguments</code>.</p>
|
||||
<pre>r = Decimal.min(x, y, z)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dmod">mod<code class='inset'>.mod(x, y) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#mod'>modulo</a></code>.</p>
|
||||
<pre>a = Decimal.mod(x, y)
|
||||
b = new Decimal(x).mod(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dmul">mul<code class='inset'>.mul(x, y) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#mul'>times</a></code>.</p>
|
||||
<pre>a = Decimal.mul(x, y)
|
||||
b = new Decimal(x).mul(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="DnoConflict">
|
||||
noConflict<code class='inset'>.noConflict() <i>⇒ Decimal constructor</i></code>
|
||||
</h5>
|
||||
<p><i>Browsers only.</i></p>
|
||||
<p>
|
||||
Reverts the <code>Decimal</code> variable to the value it had before this library was loaded
|
||||
and returns a reference to the original Decimal constructor so it can be assigned to a
|
||||
variable with a different name.
|
||||
</p>
|
||||
<pre>
|
||||
<script> Decimal = 1 </script>
|
||||
<script src='/path/to/decimal.js'></script>
|
||||
<script>
|
||||
a = new Decimal(2) // '2'
|
||||
D = Decimal.noConflict()
|
||||
Decimal // 1
|
||||
b = new D(3) // '3'
|
||||
</script></pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dpow">pow<code class='inset'>.pow(base, exponent) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>base</code>: <i>number|string|Decimal</i><br />
|
||||
<code>exponent</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href="#pow">toPower</a></code>.</p>
|
||||
<pre>a = Decimal.pow(x, y)
|
||||
b = new Decimal(x).pow(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Drandom">
|
||||
random<code class='inset'>.random([dp]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p><code>dp</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive</p>
|
||||
<p>
|
||||
Returns a new Decimal with a pseudo-random value equal to or greater than <code>0</code> and
|
||||
less than <code>1</code>.
|
||||
</p>
|
||||
<p>
|
||||
The return value will have <code>dp</code> decimal places (or less if trailing zeros are
|
||||
produced). If <code>dp</code> is omitted then the number of decimal places will
|
||||
default to the current <a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<p>
|
||||
If the value of <code>this</code> Decimal constructor's
|
||||
<a href='#crypto'><code>crypto</code></a> property is <code>true</code>, and the
|
||||
<code>crypto</code> object is available in the host environment, the random digits of the
|
||||
return value are generated by either <code>crypto.getRandomValues</code> (Web Cryptography API
|
||||
in modern browsers) or <code>crypto.randomBytes</code> (Node.js), otherwise, if the the value
|
||||
of the property is <code>false</code> the return value is generated by
|
||||
<code>Math.random</code> (fastest).
|
||||
</p>
|
||||
<p>
|
||||
If the value of <code>this</code> Decimal constructor's
|
||||
<a href='#crypto'><code>crypto</code></a> property is set <code>true</code> and the
|
||||
<code>crypto</code> object and associated method are not available, an exception will be
|
||||
thrown.
|
||||
</p>
|
||||
<p>
|
||||
If one of the <code>crypto</code> methods is used, the value of the returned Decimal should be
|
||||
cryptographically-secure and statistically indistinguishable from a random value.
|
||||
</p>
|
||||
<pre>Decimal.set({ precision: 10 })
|
||||
Decimal.random() // '0.4117936847'
|
||||
Decimal.random(20) // '0.78193327636914089009'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dround">round<code class='inset'>.round(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#round'>round</a></code>.</p>
|
||||
<pre>a = Decimal.round(x)
|
||||
b = new Decimal(x).round()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dset">set<code class='inset'>.set(object) <i>⇒ Decimal constructor</i></code></h5>
|
||||
<p><code>object</code>: <i>object</i></p>
|
||||
<p>
|
||||
Configures the 'global' settings for <code>this</code> particular Decimal constructor, i.e.
|
||||
the settings which apply to operations performed on the Decimal instances created by it.
|
||||
</p>
|
||||
<p>Returns <code>this</code> Decimal constructor.</p>
|
||||
<p>
|
||||
The configuration object, <code>object</code>, can contain some or all of the properties
|
||||
described in detail at <a href="#constructor-properties">Properties</a> and shown in the
|
||||
example below.
|
||||
</p>
|
||||
<p>
|
||||
The values of the configuration object properties are checked for validity and then stored as
|
||||
equivalently-named properties of <code>this</code> Decimal constructor.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>object</code> or configuration property value.</p>
|
||||
<pre>
|
||||
// Defaults
|
||||
Decimal.set({
|
||||
precision: 20,
|
||||
rounding: 4,
|
||||
toExpNeg: -7,
|
||||
toExpPos: 21,
|
||||
maxE: 9e15,
|
||||
minE: -9e15,
|
||||
modulo: 1,
|
||||
crypto: false
|
||||
})</pre>
|
||||
<p>
|
||||
The properties of a Decimal constructor can also be set by direct assignment, but that will
|
||||
by-pass the validity checking that this method performs - this is not a problem if the user
|
||||
knows that the assingment is valid.
|
||||
</p>
|
||||
<pre>Decimal.precision = 40</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dsign">sign<code class='inset'>.sign(x) <i>⇒ number</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<table>
|
||||
<tr><th>Returns</th><th> </th></tr>
|
||||
<tr>
|
||||
<td class='centre'><code>1</code></td>
|
||||
<td>if the value of <code>x</code> is non-zero and its sign is positive</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>-1</code></td>
|
||||
<td>if the value of <code>x</code> is non-zero and its sign is negative</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>0</code></td>
|
||||
<td>if the value of <code>x</code> is positive zero</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>-0</code></td>
|
||||
<td>if the value of <code>x</code> is negative zero</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>NaN</code></td>
|
||||
<td>if the value of <code>x</code> is <code>NaN</code></td>
|
||||
</tr>
|
||||
</table>
|
||||
<pre>r = Decimal.sign(x)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dsin">sin<code class='inset'>.sin(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#sin'>sine</a></code>.</p>
|
||||
<pre>a = Decimal.sin(x)
|
||||
b = new Decimal(x).sin()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dsinh">sinh<code class='inset'>.sinh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#sin'>hyperbolicSine</a></code>.</p>
|
||||
<pre>a = Decimal.sinh(x)
|
||||
b = new Decimal(x).sinh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dsqrt">sqrt<code class='inset'>.sqrt(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <a href='#sqrt'>squareRoot</a>.</p>
|
||||
<pre>a = Decimal.sqrt(x)
|
||||
b = new Decimal(x).sqrt()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dsub">sub<code class='inset'>.sub(x, y) <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>y</code>: <i>number|string|Decimal</i>
|
||||
</p>
|
||||
<p>See <code><a href='#sub'>minus</a></code>.</p>
|
||||
<pre>a = Decimal.sub(x, y)
|
||||
b = new Decimal(x).sub(y)
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dtan">tan<code class='inset'>.tan(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#tan'>tangent</a></code>.</p>
|
||||
<pre>a = Decimal.tan(x)
|
||||
b = new Decimal(x).tan()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dtanh">tanh<code class='inset'>.tanh(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#tan'>hyperbolicTangent</a></code>.</p>
|
||||
<pre>a = Decimal.tanh(x)
|
||||
b = new Decimal(x).tanh()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="Dtrunc">trunc<code class='inset'>.trunc(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>See <code><a href='#trunc'>truncated</a></code>.</p>
|
||||
<pre>a = Decimal.trunc(x)
|
||||
b = new Decimal(x).trunc()
|
||||
a.equals(b) // true</pre>
|
||||
|
||||
|
||||
|
||||
|
||||
<h4 id="constructor-properties">Properties</h4>
|
||||
<p>The properties of a Decimal constructor.</p>
|
||||
|
||||
|
||||
|
||||
<h6 id='configProps'>Configuration properties</h6>
|
||||
<p>
|
||||
The values of the configuration properties <a href='#precision'><code>precision</code></a>,
|
||||
<a href='#rounding'><code>rounding</code></a>, <a href='#minE'><code>minE</code></a>,
|
||||
<a href='#maxE'><code>maxE</code></a>, <a href='#toExpNeg'><code>toExpNeg</code></a>,
|
||||
<a href='#toExpPos'><code>toExpPos</code></a>, <a href='#modulo'><code>modulo</code></a>, and
|
||||
<a href='#crypto'><code>crypto</code></a> are set using the
|
||||
<a href='#Dset'><code>set</code></a> method.
|
||||
</p>
|
||||
<p>
|
||||
As simple object properties they can be set directly without using
|
||||
<a href='#Dset'><code>set</code></a>, and it is fine to do so, but the values assigned
|
||||
will not then be checked for validity. For example:
|
||||
</p>
|
||||
<pre>Decimal.set({ precision: 0 })
|
||||
// '[DecimalError] Invalid argument: precision: 0'
|
||||
|
||||
Decimal.precision = 0
|
||||
// No error is thrown and the results of calculations are unreliable</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="precision">precision</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>1</code> to <code>1e+9</code> inclusive<br />
|
||||
Default value: <code>20</code>
|
||||
</p>
|
||||
<p>The <i>maximum</i> number of significant digits of the result of an operation.</p>
|
||||
<p>
|
||||
All functions which return a Decimal will round the return value to <code>precision</code>
|
||||
significant digits except <a href='#decimal'><code>Decimal</code></a>,
|
||||
<a href='#abs'><code>absoluteValue</code></a>,
|
||||
<a href='#ceil'><code>ceil</code></a>, <a href='#floor'><code>floor</code></a>,
|
||||
<a href='#neg'><code>negated</code></a>, <a href='#round'><code>round</code></a>,
|
||||
<a href='#toDP'><code>toDecimalPlaces</code></a>,
|
||||
<a href='#toNearest'><code>toNearest</code></a> and
|
||||
<a href='#trunc'><code>truncated</code></a>.
|
||||
</p>
|
||||
<pre>Decimal.set({ precision: 5 })
|
||||
Decimal.precision // 5</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="rounding">rounding</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>0</code> to <code>8</code> inclusive<br />
|
||||
Default value: <code>4</code> <a href="#modes">(<code>ROUND_HALF_UP</code>)</a>
|
||||
</p>
|
||||
<p>
|
||||
The default rounding mode used when rounding the result of an operation to
|
||||
<code><a href='#precision'>precision</a></code> significant digits, and when rounding the
|
||||
return value of the <a href='#round'><code>round</code></a>,
|
||||
<a href='#toBinary'><code>toBinary</code></a>,
|
||||
<a href='#toDP'><code>toDecimalPlaces</code></a>,
|
||||
<a href='#toExponential'><code>toExponential</code></a>,
|
||||
<a href='#toFixed'><code>toFixed</code></a>,
|
||||
<a href='#toHexadecimal'><code>toHexadecimal</code></a>,
|
||||
<a href='#toNearest'><code>toNearest</code></a>,
|
||||
<a href='#toOctal'><code>toOctal</code></a>,
|
||||
<a href='#toPrecision'><code>toPrecision</code></a> and
|
||||
<a href='#toSD'><code>toSignificantDigits</code></a> methods.
|
||||
</p>
|
||||
<p>
|
||||
The <a href='#modes'>rounding modes</a> are available as enumerated properties of the
|
||||
constructor.
|
||||
</p>
|
||||
<pre>Decimal.set({ rounding: Decimal.ROUND_UP })
|
||||
Decimal.set({ rounding: 0 }) // equivalent
|
||||
Decimal.rounding // 0</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="minE">minE</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>-9e15</code> to <code>0</code> inclusive<br />
|
||||
Default value: <code>-9e15</code>
|
||||
</p>
|
||||
<p>
|
||||
The negative exponent limit, i.e. the exponent value below which underflow to zero occurs.
|
||||
</p>
|
||||
<p>
|
||||
If the <code>Decimal</code> to be returned by a calculation would have an exponent lower than
|
||||
<code>minE</code> then the value of that <code>Decimal</code> becomes zero.
|
||||
<p>
|
||||
JavaScript numbers underflow to zero for exponents below <code>-324</code>.
|
||||
</p>
|
||||
<pre>Decimal.set({ minE: -500 })
|
||||
Decimal.minE // -500
|
||||
new Decimal('1e-500') // '1e-500'
|
||||
new Decimal('9.9e-501') // '0'
|
||||
|
||||
Decimal.set({ minE: -3 })
|
||||
new Decimal(0.001) // '0.01' e is -3
|
||||
new Decimal(0.0001) // '0' e is -4</pre>
|
||||
<p>
|
||||
The smallest possible magnitude of a non-zero Decimal is <code>1e-9000000000000000</code>
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="maxE">maxE</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>0</code> to <code>9e15</code> inclusive<br />
|
||||
Default value: <code>9e15</code>
|
||||
</p>
|
||||
<p>
|
||||
The positive exponent limit, i.e. the exponent value above which overflow to
|
||||
<code>Infinity</code> occurs.
|
||||
</p>
|
||||
<p>
|
||||
If the <code>Decimal</code> to be returned by a calculation would have an exponent higher than
|
||||
<code>maxE</code> then the value of that <code>Decimal</code> becomes <code>Infinity</code>.
|
||||
<p>
|
||||
JavaScript numbers overflow to <code>Infinity</code> for exponents above <code>308</code>.
|
||||
</p>
|
||||
<pre>Decimal.set({ maxE: 500 })
|
||||
Decimal.maxE // 500
|
||||
new Decimal('9.999e500') // '9.999e+500'
|
||||
new Decimal('1e501') // 'Infinity'
|
||||
|
||||
Decimal.set({ maxE: 4 })
|
||||
new Decimal(99999) // '99999' e is 4
|
||||
new Decimal(100000) // 'Infinity'</pre>
|
||||
<p>
|
||||
The largest possible magnitude of a finite Decimal is <code>9.999...e+9000000000000000</code>
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="toExpNeg">toExpNeg</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>-9e15</code> to <code>0</code> inclusive<br />
|
||||
Default value: <code>-7</code>
|
||||
</p>
|
||||
<p>
|
||||
The negative exponent value at and below which <a href='#toString'><code>toString</code></a>
|
||||
returns exponential notation.
|
||||
</p>
|
||||
<pre>Decimal.set({ toExpNeg: -7 })
|
||||
Decimal.toExpNeg // -7
|
||||
new Decimal(0.00000123) // '0.00000123' e is -6
|
||||
new Decimal(0.000000123) // '1.23e-7'
|
||||
|
||||
// Always return exponential notation:
|
||||
Decimal.set({ toExpNeg: 0 })</pre>
|
||||
<p>
|
||||
JavaScript numbers use exponential notation for negative exponents of <code>-7</code> and
|
||||
below.
|
||||
</p>
|
||||
<p>
|
||||
Regardless of the value of <code>toExpNeg</code>, the
|
||||
<a href='#toFixed'><code>toFixed</code></a> method will always return a value in normal
|
||||
notation and the <a href='#toExponential'><code>toExponential</code></a> method will always
|
||||
return a value in exponential form.
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="toExpPos">toExpPos</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>0</code> to <code>9e15</code> inclusive<br />
|
||||
Default value: <code>20</code>
|
||||
</p>
|
||||
<p>
|
||||
The positive exponent value at and above which <a href='#toString'><code>toString</code></a>
|
||||
returns exponential notation.
|
||||
</p>
|
||||
<pre>Decimal.set({ toExpPos: 2 })
|
||||
Decimal.toExpPos // 2
|
||||
new Decimal(12.3) // '12.3' e is 1
|
||||
new Decimal(123) // '1.23e+2'
|
||||
|
||||
// Always return exponential notation:
|
||||
Decimal.set({ toExpPos: 0 })</pre>
|
||||
<p>
|
||||
JavaScript numbers use exponential notation for positive exponents of <code>20</code> and
|
||||
above.
|
||||
</p>
|
||||
<p>
|
||||
Regardless of the value of <code>toExpPos</code>, the
|
||||
<a href='#toFixed'><code>toFixed</code></a> method will always return a value in normal
|
||||
notation and the <a href='#toExponential'><code>toExponential</code></a> method will always
|
||||
return a value in exponential form.
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="modulo">modulo</h5>
|
||||
<p>
|
||||
<i>number</i>: integer, <code>0</code> to <code>9</code> inclusive<br />
|
||||
Default value: <code>1</code> (<code>ROUND_DOWN</code>)
|
||||
</p>
|
||||
<p>The modulo mode used when calculating the modulus: <code>a mod n</code>.</p>
|
||||
<p>
|
||||
The quotient, <code>q = a / n</code>, is calculated according to the
|
||||
<a href='#rounding'><code>rounding</code></a> mode that corresponds to the chosen
|
||||
<code>modulo</code> mode.
|
||||
</p>
|
||||
<p>The remainder, <code>r</code>, is calculated as: <code>r = a - n * q</code>.</p>
|
||||
<p>
|
||||
The modes that are most commonly used for the modulus/remainder operation are shown in the
|
||||
following table. Although the other <a href='#rounding'><code>rounding</code></a> modes can
|
||||
be used, they may not give useful results.
|
||||
</p>
|
||||
<table>
|
||||
<tr><th>Property</th><th>Value</th><th>Description</th></tr>
|
||||
<tr>
|
||||
<td>ROUND_UP</td><td class='centre'>0</td>
|
||||
<td>The remainder is positive if the dividend is negative, else is negative</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td>ROUND_DOWN</td><td class='centre'>1</td>
|
||||
<td>
|
||||
The remainder has the same sign as the dividend.<br />
|
||||
This uses truncating division and matches the behaviour of JavaScript's remainder
|
||||
operator <code>%</code>.
|
||||
</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td>ROUND_FLOOR</td><td class='centre'>3</td>
|
||||
<td>
|
||||
The remainder has the same sign as the divisor.<br />
|
||||
(This matches Python's <code>%</code> operator)
|
||||
</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td>ROUND_HALF_EVEN</td><td class='centre'>6</td>
|
||||
<td>The <i>IEEE 754</i> remainder function</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td>EUCLID</td><td class='centre'>9</td>
|
||||
<td>
|
||||
The remainder is always positive.<br />
|
||||
Euclidian division: <code>q = sign(x) * floor(a / abs(x))</code>.
|
||||
</td>
|
||||
</tr>
|
||||
</table>
|
||||
<p>
|
||||
The rounding/modulo modes are available as enumerated properties of the Decimal constructor.
|
||||
</p>
|
||||
<pre>Decimal.set({ modulo: Decimal.EUCLID })
|
||||
Decimal.set({ modulo: 9 }) // equivalent
|
||||
Decimal.modulo // 9</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="crypto">crypto</h5>
|
||||
<p>
|
||||
<i>boolean</i>: <code>true/false</code><br /> Default value: <code>false</code>
|
||||
</p>
|
||||
<p>
|
||||
The value that determines whether cryptographically-secure pseudo-random number generation is
|
||||
used.
|
||||
</p>
|
||||
<p>See <a href='#Drandom'><code>random</code></a>.</p>
|
||||
<pre>Decimal.crypto // false
|
||||
Decimal.set({ crypto: true })
|
||||
Decimal.crypto // true</pre>
|
||||
|
||||
|
||||
|
||||
<h6 id="modes">Rounding modes</h6>
|
||||
<p>
|
||||
The library's enumerated rounding modes are stored as properties of the Decimal constructor.
|
||||
<br />They are not referenced internally by the library itself.
|
||||
</p>
|
||||
<p>Rounding modes 0 to 6 (inclusive) are the same as those of Java's BigDecimal class.</p>
|
||||
<table>
|
||||
<tr><th>Property</th><th>Value</th><th>Description</th></tr>
|
||||
<tr><td><b>ROUND_UP</b></td><td class='centre'>0</td><td>Rounds away from zero</td></tr>
|
||||
<tr><td><b>ROUND_DOWN</b></td><td class='centre'>1</td><td>Rounds towards zero</td></tr>
|
||||
<tr><td><b>ROUND_CEIL</b></td><td class='centre'>2</td><td>Rounds towards Infinity</td></tr>
|
||||
<tr><td><b>ROUND_FLOOR</b></td><td class='centre'>3</td><td>Rounds towards -Infinity</td></tr>
|
||||
<tr>
|
||||
<td><b>ROUND_HALF_UP</b></td><td class='centre'>4</td>
|
||||
<td>Rounds towards nearest neighbour.<br />If equidistant, rounds away from zero</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b>ROUND_HALF_DOWN</b></td><td class='centre'>5</td>
|
||||
<td>Rounds towards nearest neighbour.<br />If equidistant, rounds towards zero</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b>ROUND_HALF_EVEN</b></td><td class='centre'>6</td>
|
||||
<td>
|
||||
Rounds towards nearest neighbour.<br />If equidistant, rounds towards even neighbour
|
||||
</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b>ROUND_HALF_CEIL</b></td><td class='centre'>7</td>
|
||||
<td>Rounds towards nearest neighbour.<br />If equidistant, rounds towards Infinity</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b>ROUND_HALF_FLOOR</b></td><td class='centre'>8</td>
|
||||
<td>Rounds towards nearest neighbour.<br />If equidistant, rounds towards -Infinity</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b>EUCLID</b></td><td class='centre'>9</td>
|
||||
<td>Not a rounding mode, see <a href='#modulo'>modulo</a></td>
|
||||
</tr>
|
||||
</table>
|
||||
<pre>Decimal.set({ rounding: Decimal.ROUND_CEIL })
|
||||
Decimal.set({ rounding: 2 }) // equivalent
|
||||
Decimal.rounding // 2</pre>
|
||||
|
||||
|
||||
|
||||
|
||||
<h3>INSTANCE</h3>
|
||||
|
||||
<h4 id="prototype-methods">Methods</h4>
|
||||
<p>The methods inherited by a Decimal instance from its constructor's prototype object.</p>
|
||||
<p>A Decimal instance is immutable in the sense that it is not changed by its methods.</p>
|
||||
<p>Methods that return a Decimal can be chained:</p>
|
||||
<pre>x = new Decimal(2).times('999.999999999999999').dividedBy(4).ceil()</pre>
|
||||
<p>Methods do not round their arguments before execution.</p>
|
||||
<p>
|
||||
The treatment of <code>±0</code>, <code>±Infinity</code> and <code>NaN</code>
|
||||
is consistent with how JavaScript treats these values.
|
||||
</p>
|
||||
<p>
|
||||
Many method names have a shorter alias. (Internally, the library always uses the shorter
|
||||
method names.)
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="abs">absoluteValue<code class='inset'>.abs() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the absolute value, i.e. the magnitude, of the value of
|
||||
this Decimal.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(-0.8)
|
||||
y = x.absoluteValue() // '0.8'
|
||||
z = y.abs() // '0.8'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="ceil">ceil<code class='inset'>.ceil() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal rounded to a whole number in
|
||||
the direction of positive <code>Infinity</code>.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.3)
|
||||
x.ceil() // '2'
|
||||
y = new Decimal(-1.8)
|
||||
y.ceil() // '-1'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="cmp">comparedTo<code class='inset'>.cmp(x) <i>⇒ number</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<table>
|
||||
<tr><th>Returns</th><th> </th></tr>
|
||||
<tr>
|
||||
<td class='centre'><code>1</code></td>
|
||||
<td>if the value of this Decimal is greater than the value of <code>x</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>-1</code></td>
|
||||
<td>if the value of this Decimal is less than the value of <code>x</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>0</code></td>
|
||||
<td>if this Decimal and <code>x</code> have the same value</td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre'><code>NaN</code></td>
|
||||
<td>if the value of either this Decimal or <code>x</code> is <code>NaN</code> </td>
|
||||
</tr>
|
||||
</table>
|
||||
<pre>
|
||||
x = new Decimal(Infinity)
|
||||
y = new Decimal(5)
|
||||
x.comparedTo(y) // 1
|
||||
x.comparedTo(x.minus(1)) // 0
|
||||
y.cmp(NaN) // NaN</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="cos">cosine<code class='inset'>.cos() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the cosine of the value in radians of this Decimal,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-1, 1</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.25)
|
||||
x.cosine() // '0.96891242171064478414'
|
||||
y = new Decimal(-0.25)
|
||||
y.cos() // '0.96891242171064478414'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="cbrt">cubeRoot<code class='inset'>.cbrt() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the cube root of this Decimal, rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits using rounding mode
|
||||
<a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The return value will be correctly rounded, i.e. rounded as if the result was first calculated
|
||||
to an infinite number of correct digits before rounding.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(125)
|
||||
x.cubeRoot() // '5'
|
||||
y = new Decimal(3)
|
||||
y.cbrt() // '1.4422495703074083823'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="dp">decimalPlaces<code class='inset'>.dp() <i>⇒ number</i></code></h5>
|
||||
<p>
|
||||
Returns the number of decimal places, i.e. the number of digits after the decimal point, of
|
||||
the value of this Decimal.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.234)
|
||||
x.decimalPlaces() // '3'
|
||||
y = new Decimal(987.654321)
|
||||
y.dp() // '6'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="div">dividedBy<code class='inset'>.div(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal divided by <code>x</code>,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(355)
|
||||
y = new Decimal(113)
|
||||
x.dividedBy(y) // '3.14159292035398230088'
|
||||
x.div(5) // '71'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="divToInt">
|
||||
dividedToIntegerBy<code class='inset'>.divToInt(x) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Return a new Decimal whose value is the integer part of dividing this Decimal by
|
||||
<code>x</code>, rounded to <code><a href='#precision'>precision</a></code> significant digits
|
||||
using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(5)
|
||||
y = new Decimal(3)
|
||||
x.dividedToIntegerBy(y) // '1'
|
||||
x.divToInt(0.7) // '7'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="eq">equals<code class='inset'>.eq(x) <i>⇒ boolean</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal equals the value of <code>x</code>,
|
||||
otherwise returns <code>false</code>.<br /> As with JavaScript, <code>NaN</code> does not
|
||||
equal <code>NaN</code>.
|
||||
</p>
|
||||
<p>Note: This method uses the <code>cmp</code> method internally.</p>
|
||||
<pre>
|
||||
0 === 1e-324 // true
|
||||
x = new Decimal(0)
|
||||
x.equals('1e-324') // false
|
||||
new Decimal(-0).eq(x) // true ( -0 === 0 )
|
||||
|
||||
y = new Decimal(NaN)
|
||||
y.equals(NaN) // false</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="floor">floor<code class='inset'>.floor() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal rounded to a whole number in
|
||||
the direction of negative <code>Infinity</code>.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.8)
|
||||
x.floor() // '1'
|
||||
y = new Decimal(-1.3)
|
||||
y.floor() // '-2'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="gt">greaterThan<code class='inset'>.gt(x) <i>⇒ boolean</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is greater than the value of
|
||||
<code>x</code>, otherwise returns <code>false</code>.
|
||||
</p>
|
||||
<p>Note: This method uses the <code>cmp</code> method internally.</p>
|
||||
<pre>
|
||||
0.1 > (0.3 - 0.2) // true
|
||||
x = new Decimal(0.1)
|
||||
x.greaterThan(Decimal(0.3).minus(0.2)) // false
|
||||
new Decimal(0).gt(x) // false</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="gte">
|
||||
greaterThanOrEqualTo<code class='inset'>.gte(x) <i>⇒ boolean</i></code>
|
||||
</h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is greater than or equal to the value
|
||||
of <code>x</code>, otherwise returns <code>false</code>.
|
||||
</p>
|
||||
<p>Note: This method uses the <code>cmp</code> method internally.</p>
|
||||
<pre>
|
||||
(0.3 - 0.2) >= 0.1 // false
|
||||
x = new Decimal(0.3).minus(0.2)
|
||||
x.greaterThanOrEqualTo(0.1) // true
|
||||
new Decimal(1).gte(x) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="cosh">hyperbolicCosine<code class='inset'>.cosh() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the hyperbolic cosine of the value in radians of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>1, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.hyperbolicCosine() // '1.5430806348152437785'
|
||||
y = new Decimal(0.5)
|
||||
y.cosh() // '1.1276259652063807852'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="sinh">hyperbolicSine<code class='inset'>.sinh() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the hyperbolic sine of the value in radians of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-Infinity, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.hyperbolicSine() // '1.1752011936438014569'
|
||||
y = new Decimal(0.5)
|
||||
y.sinh() // '0.52109530549374736162'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="tanh">hyperbolicTangent<code class='inset'>.tanh() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the hyperbolic tangent of the value in radians of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-1, 1</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.hyperbolicTangent() // '0.76159415595576488812'
|
||||
y = new Decimal(0.5)
|
||||
y.tanh() // '0.4621171572600097585'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="acos">inverseCosine<code class='inset'>.acos() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse cosine in radians of the value of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-1, 1</code>]<br />
|
||||
Range: [<code>0, pi</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0)
|
||||
x.inverseCosine() // '1.5707963267948966192'
|
||||
y = new Decimal(0.5)
|
||||
y.acos() // '1.0471975511965977462'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="acosh">
|
||||
inverseHyperbolicCosine<code class='inset'>.acosh() <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse hyperbolic cosine in radians of the value of
|
||||
this Decimal, rounded to <a href='#precision'><code>precision</code></a> significant
|
||||
digits using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>1, Infinity</code>]<br />
|
||||
Range: [<code>0, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(5)
|
||||
x.inverseHyperbolicCosine() // '2.2924316695611776878'
|
||||
y = new Decimal(50)
|
||||
y.acosh() // '4.6050701709847571595'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="asinh">
|
||||
inverseHyperbolicSine<code class='inset'>.asinh() <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse hyperbolic sine in radians of the value of
|
||||
this Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits
|
||||
using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-Infinity, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(5)
|
||||
x.inverseHyperbolicSine() // '2.3124383412727526203'
|
||||
y = new Decimal(50)
|
||||
y.asinh() // '4.6052701709914238266'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="atanh">
|
||||
inverseHyperbolicTangent<code class='inset'>.atanh() <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse hyperbolic tangent in radians of the value of
|
||||
this Decimal, rounded to <a href='#precision'><code>precision</code></a> significant
|
||||
digits using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-1, 1</code>]<br />
|
||||
Range: [<code>-Infinity, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.5)
|
||||
x.inverseHyperbolicTangent() // '0.5493061443340548457'
|
||||
y = new Decimal(0.75)
|
||||
y.atanh() // '0.97295507452765665255'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="asin">inverseSine<code class='inset'>.asin() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse sine in radians of the value of this Decimal,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-1, 1</code>]<br />
|
||||
Range: [<code>-pi/2, pi/2</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.5)
|
||||
x.inverseSine() // '0.52359877559829887308'
|
||||
y = new Decimal(0.75)
|
||||
y.asin() // '0.84806207898148100805'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="atan">inverseTangent<code class='inset'>.atan() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the inverse tangent in radians of the value of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-pi/2, pi/2</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.5)
|
||||
x.inverseTangent() // '0.46364760900080611621'
|
||||
y = new Decimal(0.75)
|
||||
y.atan() // '0.6435011087932843868'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="isFinite">isFinite<code class='inset'>.isFinite() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is a finite number, otherwise returns
|
||||
<code>false</code>.<br />
|
||||
The only possible non-finite values of a Decimal are <code>NaN</code>, <code>Infinity</code>
|
||||
and <code>-Infinity</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.isFinite() // true
|
||||
y = new Decimal(Infinity)
|
||||
y.isFinite() // false</pre>
|
||||
<p>
|
||||
Note: The native method <code>isFinite()</code> can be used if
|
||||
<code>n <= Number.MAX_VALUE</code>.
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="isInt">isInteger<code class='inset'>.isInt() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is a whole number, otherwise returns
|
||||
<code>false</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.isInteger() // true
|
||||
y = new Decimal(123.456)
|
||||
y.isInt() // false</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="isNaN">isNaN<code class='inset'>.isNaN() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is <code>NaN</code>, otherwise returns
|
||||
<code>false</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(NaN)
|
||||
x.isNaN() // true
|
||||
y = new Decimal('Infinity')
|
||||
y.isNaN() // false</pre>
|
||||
<p>Note: The native method <code>isNaN()</code> can also be used.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="isNeg">isNegative<code class='inset'>.isNeg() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is negative, otherwise returns
|
||||
<code>false</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(-0)
|
||||
x.isNegative() // true
|
||||
y = new Decimal(2)
|
||||
y.isNeg // false</pre>
|
||||
<p>Note: <code>n < 0</code> can be used if <code>n <= -Number.MIN_VALUE</code>.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="isPos">isPositive<code class='inset'>.isPos() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is positive, otherwise returns
|
||||
<code>false</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(0)
|
||||
x.isPositive() // true
|
||||
y = new Decimal(-2)
|
||||
y.isPos // false</pre>
|
||||
<p>Note: <code>n < 0</code> can be used if <code>n <= -Number.MIN_VALUE</code>.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="isZero">isZero<code class='inset'>.isZero() <i>⇒ boolean</i></code></h5>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is zero or minus zero, otherwise
|
||||
returns <code>false</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(-0)
|
||||
x.isZero() && x.isNeg() // true
|
||||
y = new Decimal(Infinity)
|
||||
y.isZero() // false</pre>
|
||||
<p>Note: <code>n == 0</code> can be used if <code>n >= Number.MIN_VALUE</code>.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="lt">lessThan<code class='inset'>.lt(x) <i>⇒ boolean</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is less than the value of
|
||||
<code>x</code>, otherwise returns <code>false</code>.
|
||||
</p>
|
||||
<p>Note: This method uses the <code>cmp</code> method internally.</p>
|
||||
<pre>
|
||||
(0.3 - 0.2) < 0.1 // true
|
||||
x = new Decimal(0.3).minus(0.2)
|
||||
x.lessThan(0.1) // false
|
||||
new Decimal(0).lt(x) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="lte">lessThanOrEqualTo<code class='inset'>.lte(x) <i>⇒ boolean</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns <code>true</code> if the value of this Decimal is less than or equal to the value of
|
||||
<code>x</code>, otherwise returns <code>false</code>.
|
||||
</p>
|
||||
<p>Note: This method uses the <code>cmp</code> method internally.</p>
|
||||
<pre>
|
||||
0.1 <= (0.3 - 0.2) // false
|
||||
x = new Decimal(0.1)
|
||||
x.lessThanOrEqualTo(Decimal(0.3).minus(0.2)) // true
|
||||
new Decimal(-1).lte(x) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="log">logarithm<code class='inset'>.log(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the base <code>x</code> logarithm of the value of this
|
||||
Decimal, rounded to <a href='#precision'><code>precision</code></a> significant digits using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>x</code> is omitted, the base 10 logarithm of the value of this Decimal will be
|
||||
returned.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1000)
|
||||
x.logarithm() // '3'
|
||||
y = new Decimal(256)
|
||||
y.log(2) // '8'</pre>
|
||||
<p>
|
||||
The return value will <i>almost always</i> be correctly rounded, i.e. rounded as if the result
|
||||
was first calculated to an infinite number of correct digits before rounding. If a result is
|
||||
incorrectly rounded the maximum error will be <code>1</code> <i>ulp</i> (unit in the last
|
||||
place).
|
||||
</p>
|
||||
<p>Logarithms to base <code>2</code> or <code>10</code> will always be correctly rounded.</p>
|
||||
<p>
|
||||
See <a href='#pow'><code>toPower</code></a> for the circumstances in which this method may
|
||||
return an incorrectly rounded result.
|
||||
</p>
|
||||
<p>The performance of this method degrades exponentially with increasing digits.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="sub">minus<code class='inset'>.minus(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal minus <code>x</code>, rounded
|
||||
to <a href='#precision'><code>precision</code></a> significant digits using rounding mode
|
||||
<a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
0.3 - 0.1 // 0.19999999999999998
|
||||
x = new Decimal(0.3)
|
||||
x.minus(0.1) // '0.2'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="mod">modulo<code class='inset'>.mod(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal modulo <code>x</code>,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The value returned, and in particular its sign, is dependent on the value of the
|
||||
<a href='#modulo'><code>modulo</code></a> property of this Decimal's constructor. If it is
|
||||
<code>1</code> (default value), the result will have the same sign as this Decimal, and it
|
||||
will match that of Javascript's <code>%</code> operator (within the limits of double
|
||||
precision) and BigDecimal's <code>remainder</code> method.
|
||||
</p>
|
||||
<p>
|
||||
See <a href='#modulo'><code>modulo</code></a> for a description of the other modulo modes.
|
||||
</p>
|
||||
<pre>
|
||||
1 % 0.9 // 0.09999999999999998
|
||||
x = new Decimal(1)
|
||||
x.modulo(0.9) // '0.1'
|
||||
|
||||
y = new Decimal(8)
|
||||
z = new Decimal(-3)
|
||||
Decimal.modulo = 1
|
||||
y.mod(z) // '2'
|
||||
Decimal.modulo = 3
|
||||
y.mod(z) // '-1'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="exp">naturalExponential<code class='inset'>.exp() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the base <code>e</code> (Euler's number, the base of the
|
||||
natural logarithm) exponential of the value of this Decimal, rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits using rounding mode
|
||||
<a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The <code><a href='#ln'>naturalLogarithm</a></code> function is the inverse of this function.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1)
|
||||
x.naturalExponential() // '2.7182818284590452354'
|
||||
y = new Decimal(2)
|
||||
y.exp() // '7.3890560989306502272'</pre>
|
||||
<p>
|
||||
The return value will be correctly rounded, i.e. rounded as if the result was first calculated
|
||||
to an infinite number of correct digits before rounding. (The mathematical result of the
|
||||
exponential function is non-terminating, unless its argument is <code>0</code>).
|
||||
</p>
|
||||
<p>The performance of this method degrades exponentially with increasing digits.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="ln">naturalLogarithm<code class='inset'>.ln() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the natural logarithm of the value of this Decimal,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The natural logarithm is the inverse of the <code><a href='#exp'>naturalExponential</a></code>
|
||||
function.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(10)
|
||||
x.naturalLogarithm() // '2.3026'
|
||||
y = new Decimal('1.23e+30')
|
||||
y.ln() // '69.28'</pre>
|
||||
<p>
|
||||
The return value will be correctly rounded, i.e. rounded as if the result was first calculated
|
||||
to an infinite number of correct digits before rounding. (The mathematical result of the
|
||||
natural logarithm function is non-terminating, unless its argument is <code>1</code>).
|
||||
</p>
|
||||
<p>
|
||||
Internally, this method is dependent on a constant whose value is the natural logarithm of
|
||||
<code>10</code>. This <code>LN10</code> variable in the source code currently has a precision
|
||||
of <code>1025</code> digits, meaning that this method can accurately calculate up to
|
||||
<code>1000</code> digits.
|
||||
</p>
|
||||
<p>
|
||||
If more than <code>1000</code> digits is required then the precision of <code>LN10</code>
|
||||
will need to be increased to <code>25</code> digits more than is required - though, as the
|
||||
time-taken by this method increases exponentially with increasing digits, it is unlikely to be
|
||||
viable to calculate over <code>1000</code> digits anyway.
|
||||
</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="neg">negated<code class='inset'>.neg() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal negated, i.e. multiplied by
|
||||
<code>-1</code>.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.8)
|
||||
x.negated() // '-1.8'
|
||||
y = new Decimal(-1.3)
|
||||
y.neg() // '1.3'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="add">plus<code class='inset'>.plus(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal plus <code>x</code>, rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits using rounding mode
|
||||
<a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
0.1 + 0.2 // 0.30000000000000004
|
||||
x = new Decimal(0.1)
|
||||
y = x.plus(0.2) // '0.3'
|
||||
new Decimal(0.7).plus(x).plus(y) // '1.1'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="sd">precision<code class='inset'>.sd([include_zeros]) <i>⇒ number</i></code></h5>
|
||||
<p>Returns the number of significant digits of the value of this Decimal.</p>
|
||||
<p>
|
||||
If <code>include_zeros</code> is <code>true</code> or <code>1</code> then any trailing zeros
|
||||
of the integer part of a number are counted as significant digits, otherwise they are not.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.234)
|
||||
x.precision() // '4'
|
||||
y = new Decimal(987000)
|
||||
y.sd() // '3'
|
||||
y.sd(true) // '6'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="round">round<code class='inset'>.round() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal rounded to a whole number using
|
||||
rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
To emulate <code>Math.round</code>, set <a href='#rounding'><code>rounding</code></a> to
|
||||
<code>7</code>, i.e. <a href='#modes'><code>ROUND_HALF_CEIL</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
Decimal.set({ rounding: 4 })
|
||||
x = 1234.5
|
||||
x.round() // '1235'
|
||||
|
||||
Decimal.rounding = Decimal.ROUND_DOWN
|
||||
x.round() // '1234'
|
||||
x // '1234.5'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="sin">sine<code class='inset'>.sin() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the sine of the value in radians of this Decimal,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-1, 1</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.5)
|
||||
x.sine() // '0.47942553860420300027'
|
||||
y = new Decimal(0.75)
|
||||
y.sin() // '0.68163876002333416673'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="sqrt">squareRoot<code class='inset'>.sqrt() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the square root of this Decimal, rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits using rounding mode
|
||||
<a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The return value will be correctly rounded, i.e. rounded as if the result was first calculated
|
||||
to an infinite number of correct digits before rounding.
|
||||
</p>
|
||||
<p>
|
||||
This method is much faster than using the <a href='#pow'><code>toPower</code></a> method with
|
||||
an exponent of <code>0.5</code>.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(16)
|
||||
x.squareRoot() // '4'
|
||||
y = new Decimal(3)
|
||||
y.sqrt() // '1.73205080756887729353'
|
||||
y.sqrt().eq( y.pow(0.5) ) // true</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="tan">tangent<code class='inset'>.tan() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the tangent of the value in radians of this Decimal,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
Domain: [<code>-Infinity, Infinity</code>]<br />
|
||||
Range: [<code>-Infinity, Infinity</code>]
|
||||
</p>
|
||||
<p>See <a href='#Pi'><code>Pi</code></a>.</p>
|
||||
<pre>
|
||||
x = new Decimal(0.5)
|
||||
x.tangent() // '0.54630248984379051326'
|
||||
y = new Decimal(0.75)
|
||||
y.tan() // '0.93159645994407246117'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="mul">times<code class='inset'>.times(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i></p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal times <code>x</code>,
|
||||
rounded to <a href='#precision'><code>precision</code></a> significant digits using rounding
|
||||
mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<pre>
|
||||
0.6 * 3 // 1.7999999999999998
|
||||
x = new Decimal(0.6)
|
||||
y = x.times(3) // '1.8'
|
||||
new Decimal('7e+500').times(y) // '1.26e+501'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toBinary">
|
||||
toBinary<code class='inset'>.toBinary([sd [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>sd</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal in binary, rounded to <code>sd</code>
|
||||
significant digits using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is defined, the return value will use binary exponential notation.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is omitted, the return value will be rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a>
|
||||
will be used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>sd</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = new Decimal(256)
|
||||
x.toBinary() // '0b100000000'
|
||||
x.toBinary(1) // '0b1p+8'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toDP">
|
||||
toDecimalPlaces<code class='inset'>.toDP([dp [, rm]]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>dp</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive.
|
||||
</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal rounded to <code>dp</code>
|
||||
decimal places using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>dp</code> is omitted, the return value will have the same value as this Decimal.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a>
|
||||
is used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>dp</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = new Decimal(12.24567)
|
||||
x.toDecimalPlaces(0) // '12'
|
||||
x.toDecimalPlaces(1, 0) // '12.3'
|
||||
|
||||
y = new Decimal(9876.54321)
|
||||
y.toDP(3) // '9876.543'
|
||||
y.toDP(1, 0) // '9876.6'
|
||||
y.toDP(1, Decimal.ROUND_DOWN) // '9876.5'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toExponential">
|
||||
toExponential<code class='inset'>.toExponential([dp [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>dp</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal in exponential notation rounded
|
||||
using rounding mode <code>rm</code> to <code>dp</code> decimal places, i.e with one digit
|
||||
before the decimal point and <code>dp</code> digits after it.
|
||||
</p>
|
||||
<p>
|
||||
If the value of this Decimal in exponential notation has fewer than <code>dp</code> fraction
|
||||
digits, the return value will be appended with zeros accordingly.
|
||||
</p>
|
||||
<p>
|
||||
If <code>dp</code> is omitted, the number of digits after the decimal point defaults to the
|
||||
minimum number of digits necessary to represent the value exactly.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a> is
|
||||
used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>dp</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = 45.6
|
||||
b = new Decimal(x)
|
||||
x.toExponential() // '4.56e+1'
|
||||
y.toExponential() // '4.56e+1'
|
||||
x.toExponential(0) // '5e+1'
|
||||
y.toExponential(0) // '5e+1'
|
||||
x.toExponential(1) // '4.6e+1'
|
||||
y.toExponential(1) // '4.6e+1'
|
||||
y.toExponential(1, 1) // '4.5e+1' (ROUND_DOWN)
|
||||
x.toExponential(3) // '4.560e+1'
|
||||
y.toExponential(3) // '4.560e+1'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toFixed">
|
||||
toFixed<code class='inset'>.toFixed([dp [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>dp</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal in normal (fixed-point) notation
|
||||
rounded to <code>dp</code> decimal places using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If the value of this Decimal in normal notation has fewer than <code>dp</code> fraction
|
||||
digits, the return value will be appended with zeros accordingly.
|
||||
</p>
|
||||
<p>
|
||||
Unlike <code>Number.prototype.toFixed</code>, which returns exponential notation if a number
|
||||
is greater or equal to <code>10<sup>21</sup></code>, this method will always return normal
|
||||
notation.
|
||||
</p>
|
||||
<p>
|
||||
If <code>dp</code> is omitted, the return value will be unrounded and in normal notation. This
|
||||
is unlike <code>Number.prototype.toFixed</code>, which returns the value to zero decimal
|
||||
places, but is useful when because of the current
|
||||
<a href="#toExpNeg"><code>toExpNeg</code></a> or
|
||||
<a href="#toExpPos"><code>toExpNeg</code></a> values,
|
||||
<code><a href='#toString'>toString</a></code> returns exponential notation.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a> is
|
||||
used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>dp</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = 3.456
|
||||
b = new Decimal(x)
|
||||
x.toFixed() // '3'
|
||||
y.toFixed() // '3.456'
|
||||
y.toFixed(0) // '3'
|
||||
x.toFixed(2) // '3.46'
|
||||
y.toFixed(2) // '3.46'
|
||||
y.toFixed(2, 1) // '3.45' (ROUND_DOWN)
|
||||
x.toFixed(5) // '3.45600'
|
||||
y.toFixed(5) // '3.45600'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toFraction">
|
||||
toFraction
|
||||
<code class='inset'>.toFraction([max_denominator]) <i>⇒ [Decimal, Decimal]</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>max_denominator</code>: <i>number|string|Decimal</i>: <code>1</code> >= integer <
|
||||
<code>Infinity</code>
|
||||
</p>
|
||||
<p>
|
||||
Returns an array of two Decimals representing the value of this Decimal as a simple fraction
|
||||
with an integer numerator and an integer denominator. The denominator will be a positive
|
||||
non-zero value less than or equal to <code>max_denominator</code>.
|
||||
</p>
|
||||
<p>
|
||||
If a maximum denominator is omitted, the denominator will be the lowest value necessary to
|
||||
represent the number exactly.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>max_denominator</code> value.</p>
|
||||
<pre>
|
||||
x = new Decimal(1.75)
|
||||
x.toFraction() // '7, 4'
|
||||
|
||||
pi = new Decimal('3.14159265358')
|
||||
pi.toFraction() // '157079632679,50000000000'
|
||||
pi.toFraction(100000) // '312689, 99532'
|
||||
pi.toFraction(10000) // '355, 113'
|
||||
pi.toFraction(100) // '311, 99'
|
||||
pi.toFraction(10) // '22, 7'
|
||||
pi.toFraction(1) // '3, 1'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toHex">
|
||||
toHexadecimal<code class='inset'>.toHex([sd [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>sd</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal in hexadecimal, rounded to
|
||||
<code>sd</code> significant digits using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is defined, the return value will use binary exponential notation.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is omitted, the return value will be rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a>
|
||||
will be used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>sd</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = new Decimal(256)
|
||||
x.toHexadecimal() // '0x100'
|
||||
x.toHex(1) // '0x1p+8'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toJSON">toJSON<code class='inset'>.toJSON() <i>⇒ string</i></code></h5>
|
||||
<p>As <a href='#valueOf'><code>valueOf</code></a>.</p>
|
||||
|
||||
|
||||
|
||||
<h5 id="toNearest">
|
||||
toNearest<code class='inset'>.toNearest(n [, rm]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>x</code>: <i>number|string|Decimal</i><br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the nearest multiple of <code>x</code> to the value of
|
||||
this Decimal.
|
||||
</p>
|
||||
<p>
|
||||
If the value of this Decimal is equidistant from two multiples of <code>x</code>, the rounding
|
||||
mode <code>rm</code>, or <a href='#rounding'><code>rounding</code></a> if <code>rm</code> is
|
||||
omitted, determines the direction of the nearest.
|
||||
</p>
|
||||
<p>
|
||||
In this context, rounding mode <a href='#rounding'><code>ROUND_HALF_UP</code></a> is
|
||||
interpreted the same as rounding mode <a href='#rounding'><code>ROUND_UP</code></a>, and so
|
||||
on, i.e. the rounding is either up, down, to ceil, to floor or to even.
|
||||
</p>
|
||||
<p>
|
||||
The return value will always have the same sign as this Decimal, unless either this Decimal
|
||||
or <code>x</code> is <code>NaN</code>, in which case the return value will be also be
|
||||
<code>NaN</code>.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(1.39)
|
||||
x.toNearest(0.25) // '1.5'
|
||||
|
||||
y = new Decimal(0.75) // equidistant from 0.5 and 1
|
||||
y.toNearest(0.5, 0) // '1' (ROUND_UP)
|
||||
y.toNearest(0.5, 1) // '0.5' (ROUND_DOWN)</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toNumber">toNumber<code class='inset'>.toNumber() <i>⇒ number</i></code></h5>
|
||||
<p>Returns the value of this Decimal converted to a primitive number.</p>
|
||||
<p>
|
||||
Type coercion with, for example, JavaScript's unary plus operator will also work, except that
|
||||
a Decimal with the value minus zero will convert to positive zero.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(456.789)
|
||||
x.toNumber() // 456.789
|
||||
+x // 456.789
|
||||
|
||||
y = new Decimal('45987349857634085409857349856430985')
|
||||
y.toNumber() // 4.598734985763409e+34
|
||||
|
||||
z = new Decimal(-0)
|
||||
1 / +z // Infinity
|
||||
1 / z.toNumber() // -Infinity</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toOctal">
|
||||
toOctal<code class='inset'>.toOctal([sd [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>sd</code>: <i>number</i>: integer, <code>0</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal in octal, rounded to <code>sd</code>
|
||||
significant digits using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is defined, the return value will use binary exponential notation.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is omitted, the return value will be rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a>
|
||||
will be used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>sd</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = new Decimal(256)
|
||||
x.toOctal() // '0o400'
|
||||
x.toOctal(1) // '0o1p+8'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="pow">toPower<code class='inset'>.pow(x) <i>⇒ Decimal</i></code></h5>
|
||||
<p><code>x</code>: <i>number|string|Decimal</i>: integer or non-integer</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal raised to the power
|
||||
<code>x</code>, rounded to <a href='#precision'><code>precision</code></a> significant digits
|
||||
using rounding mode <a href='#rounding'><code>rounding</code></a>.
|
||||
</p>
|
||||
<p>
|
||||
The performance of this method degrades exponentially with increasing digits. For
|
||||
non-integer exponents in particular, the performance of this method may not be adequate.
|
||||
</p>
|
||||
<pre>
|
||||
Math.pow(0.7, 2) // 0.48999999999999994
|
||||
x = new Decimal(0.7)
|
||||
x.toPower(2) // '0.49'
|
||||
new Decimal(3).pow(-2) // '0.11111111111111111111'
|
||||
|
||||
new Decimal(1217652.23).pow('98765.489305603941')
|
||||
// '4.8227010515242461181e+601039'</pre>
|
||||
<p><i>Is the pow function guaranteed to be correctly rounded?</i></p>
|
||||
<p>
|
||||
The return value will <i>almost always</i> be correctly rounded, i.e. rounded as if the result
|
||||
was first calculated to an infinite number of correct digits before rounding. If a result is
|
||||
incorrectly rounded the maximum error will be <code>1</code> <i>ulp</i> (unit in the last
|
||||
place).
|
||||
</p>
|
||||
<p>For non-integer and larger exponents this method uses the formula</p>
|
||||
<blockquote><code>x<sup>y</sup> = exp(y*ln(x))</code></blockquote>
|
||||
<p>
|
||||
As the mathematical return values of the <a href='#exp'><code>exp</code></a> and
|
||||
<a href='#ln'><code>ln</code></a> functions are both non-terminating (excluding arguments of
|
||||
<code>0</code> or <code>1</code>), the values of the Decimals returned by the functions as
|
||||
implemented by this library will necessarily be rounded approximations, which means that there
|
||||
can be no guarantee of correct rounding when they are combined in the above formula.
|
||||
</p>
|
||||
<p>
|
||||
The return value may, depending on the rounding mode, be incorrectly rounded only if the first
|
||||
<code>15</code> rounding digits are <code>15</code> zeros (and there are non-zero digits
|
||||
following at some point), or <code>15</code> nines, or a <code>5</code> or <code>4</code>
|
||||
followed by <code>14</code> nines.
|
||||
</p>
|
||||
<p>
|
||||
Therefore, assuming the first <code>15</code> rounding digits are each equally likely to be
|
||||
any digit, <code>0-9</code>, the probability of an incorrectly rounded result is less than
|
||||
<code>1</code> in <code>250,000,000,000,000</code>.
|
||||
</p>
|
||||
<p>
|
||||
An example of incorrect rounding:
|
||||
</p>
|
||||
<pre>
|
||||
Decimal.set({ precision: 20, rounding: 1 })
|
||||
new Decimal(28).pow('6.166675020000903537297764507632802193308677149')
|
||||
// 839756321.64088511</pre>
|
||||
<p>As the exact mathematical result begins</p>
|
||||
<pre>839756321.6408851099999999999999999999999999998969466049426031167...</pre>
|
||||
<p>
|
||||
and the rounding mode is set to <code><a href='#modes'>ROUND_DOWN</a></code>, the correct
|
||||
return value should be
|
||||
</p>
|
||||
<pre>839756321.64088510999</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toPrecision">
|
||||
toPrecision<code class='inset'>.toPrecision([sd [, rm]]) <i>⇒ string</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>sd</code>: <i>number</i>: integer, <code>1</code> to <code>1e+9</code> inclusive<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive
|
||||
</p>
|
||||
<p>
|
||||
Returns a string representing the value of this Decimal rounded to <code>sd</code> significant
|
||||
digits using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is less than the number of digits necessary to represent the integer part
|
||||
of the value in normal (fixed-point) notation, then exponential notation is used.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is omitted, the return value is the same as
|
||||
<code><a href='#toString'>toString</a></code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a> is
|
||||
used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>sd</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
x = 45.6
|
||||
b = new Decimal(x)
|
||||
x.toPrecision() // '45.6'
|
||||
y.toPrecision() // '45.6'
|
||||
x.toPrecision(1) // '5e+1'
|
||||
y.toPrecision(1) // '5e+1'
|
||||
y.toPrecision(2, 0) // '4.6e+1' (ROUND_UP)
|
||||
y.toPrecision(2, 1) // '4.5e+1' (ROUND_DOWN)
|
||||
x.toPrecision(5) // '45.600'
|
||||
y.toPrecision(5) // '45.600'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toSD">
|
||||
toSignificantDigits<code class='inset'>.toSD([sd [, rm]]) <i>⇒ Decimal</i></code>
|
||||
</h5>
|
||||
<p>
|
||||
<code>sd</code>: <i>number</i>: integer, <code>1</code> to <code>1e+9</code> inclusive.<br />
|
||||
<code>rm</code>: <i>number</i>: integer, <code>0</code> to <code>8</code> inclusive.
|
||||
</p>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal rounded to <code>sd</code>
|
||||
significant digits using rounding mode <code>rm</code>.
|
||||
</p>
|
||||
<p>
|
||||
If <code>sd</code> is omitted, the return value will be rounded to
|
||||
<a href='#precision'><code>precision</code></a> significant digits.
|
||||
</p>
|
||||
<p>
|
||||
If <code>rm</code> is omitted, rounding mode <a href='#rounding'><code>rounding</code></a>
|
||||
will be used.
|
||||
</p>
|
||||
<p>Throws on an invalid <code>sd</code> or <code>rm</code> value.</p>
|
||||
<pre>
|
||||
Decimal.set({ precision: 5, rounding: 4 })
|
||||
x = new Decimal(9876.54321)
|
||||
|
||||
x.toSignificantDigits() // '9876.5'
|
||||
x.toSignificantDigits(6) // '9876.54'
|
||||
x.toSignificantDigits(6, Decimal.ROUND_UP) // '9876.55'
|
||||
x.toSD(2) // '9900'
|
||||
x.toSD(2, 1) // '9800'
|
||||
x // '9876.54321'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="toString">toString<code class='inset'>.toString() <i>⇒ string</i></code></h5>
|
||||
<p>Returns a string representing the value of this Decimal.</p>
|
||||
<p>
|
||||
If this Decimal has a positive exponent that is equal to or greater than
|
||||
<a href="#toExpPos"><code>toExpPos</code></a>, or a negative exponent equal to or less than
|
||||
<a href="#toExpPos"><code>toExpNeg</code></a>, then exponential notation will be returned.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(750000)
|
||||
x.toString() // '750000'
|
||||
Decimal.set({ toExpPos: 5 })
|
||||
x.toString() // '7.5e+5'
|
||||
|
||||
Decimal.set({ precision: 4 })
|
||||
y = new Decimal('1.23456789')
|
||||
y.toString() // '1.23456789'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="trunc">truncated<code class='inset'>.trunc() <i>⇒ Decimal</i></code></h5>
|
||||
<p>
|
||||
Returns a new Decimal whose value is the value of this Decimal truncated to a whole number.
|
||||
</p>
|
||||
<p>
|
||||
The return value is not affected by the value of the
|
||||
<a href='#precision'><code>precision</code></a> setting.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(123.456)
|
||||
x.truncated() // '123'
|
||||
y = new Decimal(-12.3)
|
||||
y.trunc() // '-12'</pre>
|
||||
|
||||
|
||||
|
||||
<h5 id="valueOf">valueOf<code class='inset'>.valueOf() <i>⇒ string</i></code></h5>
|
||||
<p>As <a href='#toString'><code>toString</code></a>, but zero is signed.</p>
|
||||
<pre>
|
||||
x = new Decimal(-0)
|
||||
x.valueOf() // '-0'</pre>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<h4 id="instance-properties">Properties</h4>
|
||||
<p>
|
||||
The value of a Decimal is stored in a normalised base <code>10000000</code> floating point
|
||||
format.
|
||||
</p>
|
||||
<p>
|
||||
A Decimal instance is an object with three properties:
|
||||
</p>
|
||||
<table>
|
||||
<tr>
|
||||
<th>Property</th>
|
||||
<th>Description</th>
|
||||
<th>Type</th>
|
||||
<th>Value</th>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre' id='digits'><b>d</b></td>
|
||||
<td>digits</td>
|
||||
<td><i>number</i><code style='color:#000'>[]</code></td>
|
||||
<td> Array of integers, each <code>0</code> - <code>1e7</code>, or <code>null</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre' id='exponent'><b>e</b></td>
|
||||
<td>exponent</td>
|
||||
<td><i>number</i></td>
|
||||
<td>Integer, <code>-9e15</code> to <code>9e15</code> inclusive, or <code>NaN</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td class='centre' id='sign'><b>s</b></td>
|
||||
<td>sign</td>
|
||||
<td><i>number</i></td>
|
||||
<td><code>-1</code>, <code>1</code>, or <code>NaN</code></td>
|
||||
</tr>
|
||||
</table>
|
||||
<p>The properties are best considered to be read-only.</p>
|
||||
<p>
|
||||
As with JavaScript numbers, the original exponent and fractional trailing zeros of a number
|
||||
are not preserved.
|
||||
</p>
|
||||
<pre>
|
||||
x = new Decimal(0.123) // '0.123'
|
||||
x.toExponential() // '1.23e-1'
|
||||
x.d // [ 1230000 ]
|
||||
x.e // -1
|
||||
x.s // 1
|
||||
|
||||
y = new Number(-123.4567000e+2) // '-12345.67'
|
||||
y.toExponential() // '-1.234567e+4'
|
||||
z = new Decimal('-123.4567000e+2') // '-12345.67'
|
||||
z.toExponential() // '-1.234567e+4'
|
||||
z.d // [ 12345, 6700000 ]
|
||||
z.e // 4
|
||||
z.s // -1</pre>
|
||||
|
||||
|
||||
|
||||
<h4 id="zero-nan-infinity">Zero, NaN and Infinity</h4>
|
||||
<p>
|
||||
The table below shows how <code>±0</code>, <code>NaN</code> and
|
||||
<code>±Infinity</code> are stored.
|
||||
</p>
|
||||
<table>
|
||||
<tr>
|
||||
<th> </th>
|
||||
<th>±0</th>
|
||||
<th>NaN</th>
|
||||
<th>±Infinity</th>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b> d </b></td>
|
||||
<td><code>[0]</code></td>
|
||||
<td><code>null</code></td>
|
||||
<td><code>null</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b> e </b></td>
|
||||
<td><code>0</code></td>
|
||||
<td><code>NaN</code></td>
|
||||
<td><code>NaN</code></td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td><b> s </b></td>
|
||||
<td><code>±1</code></td>
|
||||
<td><code>NaN</code></td>
|
||||
<td><code>±1</code></td>
|
||||
</tr>
|
||||
</table>
|
||||
<pre>
|
||||
x = new Number(-0) // 0
|
||||
1 / x == -Infinity // true
|
||||
|
||||
y = new Decimal(-0)
|
||||
y.d // '0' ( [0].toString() )
|
||||
y.e // 0
|
||||
y.s // -1
|
||||
y.toString() // '0'
|
||||
y.valueOf() // '-0'</pre>
|
||||
|
||||
|
||||
|
||||
<h4 id='Errors'>Errors</h4>
|
||||
<p>
|
||||
The errors that are thrown are generic <code>Error</code> objects whose <code>message</code>
|
||||
property begins with <code>"[DecimalError]"</code>.
|
||||
</p>
|
||||
<p>To determine if an exception is a Decimal Error:</p>
|
||||
<pre>
|
||||
try {
|
||||
// ...
|
||||
} catch (e) {
|
||||
if ( e instanceof Error && /DecimalError/.test(e.message) ) {
|
||||
// ...
|
||||
}
|
||||
}</pre>
|
||||
|
||||
|
||||
|
||||
<h4 id='Pi'>Pi</h4>
|
||||
<p>
|
||||
The maximum precision of the trigonometric methods is dependent on the internal value of the
|
||||
constant pi, which is defined as the string <code>PI</code> near the top of the source file.
|
||||
</p>
|
||||
<p>
|
||||
It has a precision of <code>1025</code> digits, meaning that the trigonometric methods
|
||||
can accurately calculate up to at least <code>1000</code> digits.
|
||||
</p>
|
||||
<p>
|
||||
If greater precision is required then the value of <code>PI</code> will need to be extended to
|
||||
about <code>25</code> digits more than the precision required.
|
||||
</p>
|
||||
<p>The value can also be shortened to reduce the size of the source file.</p>
|
||||
<p>To get the value of pi:</p>
|
||||
<pre>
|
||||
pi = Decimal.acos(-1)</pre>
|
||||
|
||||
|
||||
|
||||
<h2 id='faq'>FAQ</h2>
|
||||
<h6>Why are trailing fractional zeros removed from Decimals?</h6>
|
||||
<p>
|
||||
Some arbitrary-precision libraries retain trailing fractional zeros as they can indicate the
|
||||
precision of a value. This can be useful but the results of arithmetic operations can be
|
||||
misleading.
|
||||
</p>
|
||||
<pre>
|
||||
x = new BigDecimal("1.0")
|
||||
y = new BigDecimal("1.1000")
|
||||
z = x.add(y) // 2.1000
|
||||
|
||||
x = new BigDecimal("1.20")
|
||||
y = new BigDecimal("3.45000")
|
||||
z = x.multiply(y) // 4.1400000</pre>
|
||||
<p>
|
||||
To specify the precision of a value is to specify that the value lies
|
||||
within a certain range.
|
||||
</p>
|
||||
<p>
|
||||
In the first example, <code>x</code> has a value of <code>1.0</code>. The trailing zero shows
|
||||
the precision of the value, implying that it is in the range <code>0.95</code> to
|
||||
<code>1.05</code>. Similarly, the precision indicated by the trailing zeros of <code>y</code>
|
||||
indicates that the value is in the range <code>1.09995</code> to <code>1.10005</code>.
|
||||
</p>
|
||||
<p>
|
||||
If we add the two lowest values in the ranges we have, <code>0.95 + 1.09995 = 2.04995</code>,
|
||||
and if we add the two highest values we have, <code>1.05 + 1.10005 = 2.15005</code>, so the
|
||||
range of the result of the addition implied by the precision of its operands is
|
||||
<code>2.04995</code> to <code>2.15005</code>.
|
||||
</p>
|
||||
<p>
|
||||
The result given by BigDecimal of <code>2.1000</code> however, indicates that the value is in
|
||||
the range <code>2.09995</code> to <code>2.10005</code> and therefore the precision implied by
|
||||
its trailing zeros may be misleading.
|
||||
</p>
|
||||
<p>
|
||||
In the second example, the true range is <code>4.122744</code> to <code>4.157256</code> yet
|
||||
the BigDecimal answer of <code>4.1400000</code> indicates a range of <code>4.13999995</code>
|
||||
to <code>4.14000005</code>. Again, the precision implied by the trailing zeros may be
|
||||
misleading.
|
||||
</p>
|
||||
<p>
|
||||
This library, like binary floating point and most calculators, does not retain trailing
|
||||
fractional zeros. Instead, the <code>toExponential</code>, <code>toFixed</code> and
|
||||
<code>toPrecision</code> methods enable trailing zeros to be added if and when required.<br />
|
||||
</p>
|
||||
</div>
|
||||
|
||||
</body>
|
||||
</html>
|
||||
1
nodered/rootfs/data/node_modules/decimal.js/doc/decimal.js.map
generated
vendored
Normal file
1
nodered/rootfs/data/node_modules/decimal.js/doc/decimal.js.map
generated
vendored
Normal file
File diff suppressed because one or more lines are too long
62
nodered/rootfs/data/node_modules/decimal.js/package.json
generated
vendored
Normal file
62
nodered/rootfs/data/node_modules/decimal.js/package.json
generated
vendored
Normal file
@@ -0,0 +1,62 @@
|
||||
{
|
||||
"_from": "decimal.js@7.1.1",
|
||||
"_id": "decimal.js@7.1.1",
|
||||
"_inBundle": false,
|
||||
"_integrity": "sha1-GtytfXDXqRxCbXVvHrZWbDvmy88=",
|
||||
"_location": "/decimal.js",
|
||||
"_phantomChildren": {},
|
||||
"_requested": {
|
||||
"type": "version",
|
||||
"registry": true,
|
||||
"raw": "decimal.js@7.1.1",
|
||||
"name": "decimal.js",
|
||||
"escapedName": "decimal.js",
|
||||
"rawSpec": "7.1.1",
|
||||
"saveSpec": null,
|
||||
"fetchSpec": "7.1.1"
|
||||
},
|
||||
"_requiredBy": [
|
||||
"/mathjs"
|
||||
],
|
||||
"_resolved": "https://registry.npmjs.org/decimal.js/-/decimal.js-7.1.1.tgz",
|
||||
"_shasum": "1adcad7d70d7a91c426d756f1eb6566c3be6cbcf",
|
||||
"_spec": "decimal.js@7.1.1",
|
||||
"_where": "/data/node_modules/mathjs",
|
||||
"author": {
|
||||
"name": "Michael Mclaughlin",
|
||||
"email": "M8ch88l@gmail.com"
|
||||
},
|
||||
"bugs": {
|
||||
"url": "https://github.com/MikeMcl/decimal.js/issues"
|
||||
},
|
||||
"bundleDependencies": false,
|
||||
"deprecated": false,
|
||||
"description": "An arbitrary-precision Decimal type for JavaScript.",
|
||||
"homepage": "https://github.com/MikeMcl/decimal.js#readme",
|
||||
"keywords": [
|
||||
"arbitrary",
|
||||
"precision",
|
||||
"arithmetic",
|
||||
"big",
|
||||
"number",
|
||||
"decimal",
|
||||
"float",
|
||||
"biginteger",
|
||||
"bigdecimal",
|
||||
"bignumber",
|
||||
"bigint",
|
||||
"bignum"
|
||||
],
|
||||
"license": "MIT",
|
||||
"main": "decimal.js",
|
||||
"name": "decimal.js",
|
||||
"repository": {
|
||||
"type": "git",
|
||||
"url": "git+https://github.com/MikeMcl/decimal.js.git"
|
||||
},
|
||||
"scripts": {
|
||||
"build": "uglifyjs decimal.js --source-map doc/decimal.js.map -c -m -o decimal.min.js --preamble \"/* decimal.js v7.1.1 https://github.com/MikeMcl/decimal.js/LICENCE */\"",
|
||||
"test": "node ./test/test.js"
|
||||
},
|
||||
"version": "7.1.1"
|
||||
}
|
||||
Reference in New Issue
Block a user